
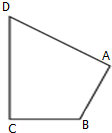
 如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )
如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )| A. | 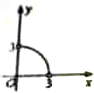 | B. | 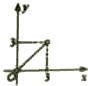 | C. | 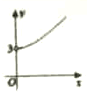 | D. |  |
分析 由已知条件便可得到∠BCD=∠BAD=90°,连接BD后便得到x2+16=y2+25,从而解出y=$\sqrt{{x}^{2}-9}$,并且得到该函数的定义域为[3,+∞),而符合这一点的只有选项D.
解答 解:根据已知条件知AB⊥AD,CB⊥CD,连接BD,则: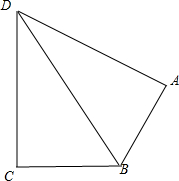
$|\overrightarrow{CB}{|}^{2}+|\overrightarrow{CD}{|}^{2}=|\overrightarrow{AB}{|}^{2}+|\overrightarrow{AD}{|}^{2}$;
∴x2+16=y2+25;
∴$y=\sqrt{{x}^{2}-9}$;
∵y>0,∴x>3;
∴符合的只有D.
故选:D.
点评 考查向量垂直的充要条件,直角三角形边的关系,而在解y时注意y的范围,并根据y的范围得出x的范围.


科目:高中数学 来源: 题型:解答题
 点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.
点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.
4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
在一次篮球定点投篮训练中,规定每人最多投3次.在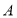 处每投进一球得3分;在
处每投进一球得3分;在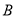 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在 处的投中率
处的投中率 ,在
,在 处的投中率为
处的投中率为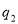 .该同学选择先在
.该同学选择先在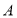 处投一球,以后都在
处投一球,以后都在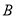 处投,且每次投篮都互不影响.用
处投,且每次投篮都互不影响.用 表示
表示
该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求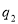 的值;
的值;
(2)求随机变量 的数学期望
的数学期望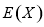 ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com