
分析 (1)运用完全平方公式,即可得到极限;
(2)分子分母同除以x2,即可得到极限;
(3)运用平方差公式,即可得到极限.
解答 解:(1)$\underset{lim}{x→0}$$\frac{{x}^{2}-2x+1}{x-1}$=$\underset{lim}{x→0}$$\frac{(x-1)^{2}}{x-1}$=$\underset{lim}{x→0}$(x-1)=-1;
(2)$\underset{lim}{x→∞}$$\frac{2{x}^{2}-1}{1+{x}^{2}}$=$\underset{lim}{x→∞}$$\frac{2-\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}$=$\frac{2-0}{1+0}$=2;
(3)$\underset{lim}{x→1}$$\frac{x-1}{\sqrt{x}-1}$=$\underset{lim}{x→1}$$\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}-1}$=$\underset{lim}{x→1}$($\sqrt{x}$+1)=1+1=2.
点评 本题考查函数极限的求法,注意运用因式分解和常见函数的极限,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
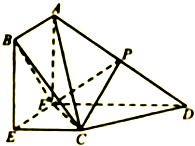 如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.
如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| C. | 命题“?x∈R,ax+b≤0”的否定是“?x∈R,ax+b>0” | |
| D. | 若ξ~B(8,0.125),则Eξ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{2},1)$ | B. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{3},\frac{1}{2})$ | C. | $(-\frac{1}{2},-\frac{1}{3})$和$(\frac{1}{2},1)$ | D. | $(-\frac{1}{3},-\frac{1}{4})$和$(\frac{1}{3},\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com