
分析 ①,f(0+x)+f(0-x)=2,得a=0,b=1,满足“准奇函数”的定义;
②,根据函数“准奇函数”的定义,利用函数奇偶性的定义即可证明函数F(x)=f(x+a)-f(a)为R上的奇函数;
③f($\frac{kπ}{2}+\frac{π}{6}$+x)+f($\frac{kπ}{2}+\frac{π}{6}$-x)=2,得a=$\frac{kπ}{2}+\frac{π}{6}$,b=1
④,f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,得点(1,2)为函数f(x)的“中心点”.
解答 解:对于①,∵函数f(x)=sinx+1,∴f(0+x)+f(0-x)=2,∴a=0,b=1,满足“准奇函数”的定义,故①正确;
对于②,若F(x)=f(x+a)-f(a),则F(-x)+F(x)=f(x+a)-f(a)+f(-x+a)-f(a)=f(a-x)+f(a+x)-2f(a),
∵f(x)在R上的“中心点”为(a,f(a)),∴f(a-x)+f(a+x)=2f(a),即F(-x)+F(x)=f(a-x)+f(a+x)-2f(a)=0,
∴F(-x)=-F(x),∴函数F(x)=f(x+a)-f(a)为R上的奇函数,∴故②正确;
对于③,f($\frac{kπ}{2}+\frac{π}{6}$+x)+f($\frac{kπ}{2}+\frac{π}{6}$-x)=2,得a=$\frac{kπ}{2}+\frac{π}{6}$,b=1,故错
对于④,函数f(x)=x3-3x2+6x-2,∴f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,
∴点(1,2)为函数f(x)的“中心点”,故④正确.
故答案为:①②④
点评 本题主要考查函数中心的定义的应用,综合性较强,运算量量较大,难度较大


科目:高中数学 来源: 题型:填空题
 某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.
某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
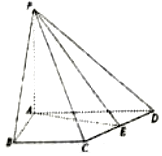 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{19}{5}$ | B. | $\frac{19}{5}$ | C. | $\frac{11}{3}$ | D. | $-\frac{11}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
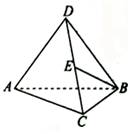 如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )
如图,在三棱锥D-ABC中,∠ABC=90°,平面DAB⊥平面ABC,DA=AB=DB=BC,E是DC的中点,则AC与BE所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{15}}}{16}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com