
分析 (1)求出f′(x)=-xsinx-acosx,当x∈(0,$\frac{π}{2}$)时,f′(x)<0,由此能证明当$x∈[0,\frac{π}{2}]$时,f(x)≤f(0)=0成立.
(2)设p(x)=f′(x),则p′(x)=-xcosx+(a-1)sinx,由导数性质得p(x)在[$\frac{π}{2}$,π]上单调递增,从而f′(x)在[0,π]上存在唯一零点β,由此推导出当x∈[0,π]时,f(x)有唯一极值点β,且β为极小值点.
(3)当x∈[0,π]时,h(a)=f(x)min=f(β),f′(β)=-βsinβ-acosβ,α=-$\frac{βsinβ}{cosβ}$,从而h(a)=$\frac{β}{cosβ}-sinβ$,设q(x)=-$\frac{xsinx}{cosx}$,则${q}^{'}(x)=-\frac{sin2x+2x}{2co{s}^{2}x}$,由此利用构造法及导数性质能求出函数h(a)的值域.
解答 证明:(1)∵f(x)=xcosx-(a+1)sinx,x∈[0,π],
∴f′(x)=-xsinx-acosx,
∵$\frac{3π}{4}≤α≤\frac{{2\sqrt{3}π}}{3}$,∴当x∈(0,$\frac{π}{2}$)时,f′(x)<0,
∴f(x)在[0,$\frac{π}{2}$]上是减函数,
∴当$x∈[0,\frac{π}{2}]$时,f(x)≤f(0)=0成立.
解:(2)f(x)有唯一极值点.
理由如下:
设p(x)=f′(x),则p′(x)=-xcosx+(a-1)sinx,
∵a≥$\frac{3π}{4}$>1,∴当x∈($\frac{π}{2}$.π)时,p′(x)>0,
∴p(x)在[$\frac{π}{2}$,π]上单调递增,
∵p(x)在[$\frac{π}{2}$,π]上存在唯一零点β,
又由(1)知,当x∈[0,$\frac{π}{2}$]时,p(x)<0,
∴p(x)在[0,$\frac{π}{2}$]上无零点,
∴f′(x)在[0,π]上存在唯一零点β,
∴当x∈(0,β)时,f′(x)<0,当x∈(β,π)时,f′(x)>0.
∴当x∈[0,π]时,f(x)有唯一极值点β,且β为极小值点.
(3)由(2)知,当x∈[0,π]时,h(a)=f(x)min=f(β),
f′(β)=-βsinβ-acosβ,
∵β∈($\frac{π}{2},π$),∴cosβ<0,∴α=-$\frac{βsinβ}{cosβ}$,
∴h(a)=f(β)=βcosβ-(a+1)sinβ=βcosβ+$\frac{βsi{n}^{2}β}{cosβ}-sinβ=\frac{β}{cosβ}-sinβ$,
设q(x)=-$\frac{xsinx}{cosx}$,则${q}^{'}(x)=-\frac{sin2x+2x}{2co{s}^{2}x}$,
当x∈($\frac{π}{2}$,π)时,sin2x+2x>-1+π>0,∴q′(x)<0,即q(x)在($\frac{π}{2},π$)单调递减,
又∵$\frac{3π}{4}≤a≤\frac{2\sqrt{3}π}{2}$时,$\frac{2π}{3}≤β≤\frac{3π}{4}$.
∴对于每一个α∈[$\frac{3π}{4},\frac{2\sqrt{3}π}{3}$],均存在唯一的β∈[$\frac{2π}{3},\frac{3π}{4}$]与之相对应,
反之亦然,
设φ(x)=$\frac{x}{cosx}-sinx$,x∈[$\frac{2π}{3}$,$\frac{3π}{4}$],
则φ′(x)=$\frac{cosx+xsinx}{co{s}^{2}x}$-cosx=$\frac{(1-co{s}^{2}x)+xsinx}{co{s}^{2}x}$=$\frac{(sin2x+2x)six}{2co{s}^{2}x}$>0,
φ(x)在[$\frac{2π}{3}$,$\frac{3π}{4}$]上单调递增,
∴当$\frac{3π}{4}≤α≤\frac{2\sqrt{3}π}{3}$时,f(β)min=φ($\frac{2π}{3}$)=-$\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$,f(β)maxφ($\frac{3π}{4}$)=-$\frac{3\sqrt{2}π}{4}$-$\frac{\sqrt{2}}{2}$.
∴函数h(a)的值域为[$-\frac{4π}{3}-\frac{\sqrt{3}}{2}$,-$\frac{3\sqrt{2}π}{4}-\frac{\sqrt{2}}{2}$].
点评 本题考查导数及其应用等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查转化化归思想、分类讨论思想、函数与方程思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
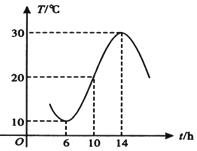 如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).
如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
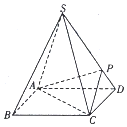 如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com