
分析 求出原函数的导函数,求得极小值点判断①;由极小值点处的函数值大于0判断②;构造函数,利用导数研究函数的单调性判断③;构造函数,利用导数研究函数的单调性判断④.
解答 解:$f(x)=\frac{2}{x}+lnx$,则f′(x)=$-\frac{2}{{x}^{2}}+\frac{1}{x}=\frac{x-2}{{x}^{2}}$(x>0),
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0,
∴f(x)在(0,2)上单调递减,在(2,+∞)上单调递增,
∴x=2是f(x)的极小值点,故①正确;
∵f(2)=1+ln2>0,∴函数f(x)在(0,+∞)上无零点,故②错误;
若使得f(x)>kx恒成立,即$\frac{2}{x}+lnx>kx$恒成立,也就是k<$\frac{2}{{x}^{2}}+\frac{lnx}{x}$恒成立,
令g(x)=$\frac{2}{{x}^{2}}+\frac{lnx}{x}$,则g′(x)=$\frac{-4x}{{x}^{4}}+\frac{1-lnx}{{x}^{2}}$=$\frac{-4}{{x}^{3}}+\frac{1-lnx}{{x}^{2}}=\frac{x-xlnx-4}{{x}^{3}}$,
再令h(x)=x-xlnx-4,
则h′(x)=-lnx,由h′(x)=0,得x=1,
∴h(x)≤h(1)<0,则g′(x)<0,
∴g(x)在(0,+∞)上单调递减,g(x)无最小值,
∴不存在正实数k,使得f(x)>kx恒成立,故③错误;
对任意两个正实数x1,x2,且x1<x2,
∵f(x)在(0,2)上单调递减,在(2,+∞)上单调递增,
若f(x1)=f(x2),则x1+x2>4,正确.
事实上,不妨设0<x1<2<x2,
则4-x1>2,而f(4-x1)-f(x2)
=f(4-x1)-f(x1)
=$\frac{2}{4-{x}_{1}}$+ln(4-x1)-$\frac{2}{{x}_{1}}$-ln(x1)=$\frac{4({x}_{1}-2)}{(4-{x}_{1}){x}_{1}}$+ln$\frac{4-{x}_{1}}{{x}_{1}}$,
令$\frac{4-{x}_{1}}{{x}_{1}}=t$,则t>1,x1=$\frac{4}{1+t}$,
故原式=F(t)=$\frac{1-{t}^{2}}{2t}$+lnt,
故F′(t)=$\frac{-{t}^{2}+2t-1}{2{t}^{2}}$<0,
故F(t)=$\frac{1-{t}^{2}}{2t}$+lnt在(1,+∞)上是减函数,
故F(t)<F(1)=0,
故f(4-x1)-f(x2)<0,
又∵f(x)在(1,+∞)上单调递增,
∴4-x1<x2,故x1+x2>4,故④为真命题.
∴真命题有①④.
故答案为:①④.
点评 本题考查命题的真假判断与应用,考查了利用导数研究函数的单调性,考查利用导数求函数的最值,是难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
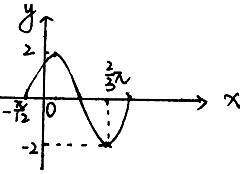 若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示
若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
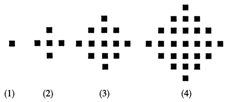 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com