
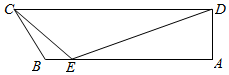
 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.分析 (Ⅰ)在△CBE中,正弦定理求出sin∠BCE;
(Ⅱ)在△CBE中,由余弦定理得CE2=BE2+CB2-2BE•CBcos120°,得CB.由余弦定理得CB2=BE2+CE2-2BE•CEcos∠BEC⇒cos∠BEC⇒sin∠BEC、cos∠AED在直角△ADE中,求得DE=2$\sqrt{7}$,在△CED中,由余弦定理得CD2=CE2+DE2-2CE•DEcos120°即可
解答 解:(Ⅰ)在△CBE中,由正弦定理得$\frac{CE}{sinB}=\frac{BE}{sin∠BCE}$,sin∠BCE=$\frac{BEsinB}{CE}=\frac{1×\frac{\sqrt{3}}{2}}{\sqrt{7}}=\frac{\sqrt{21}}{14}$,
(Ⅱ)在△CBE中,由余弦定理得CE2=BE2+CB2-2BE•CBcos120°,即7=1+CB2+CB,解得CB=2.
由余弦定理得CB2=BE2+CE2-2BE•CEcos∠BEC⇒cos∠BEC=$\frac{2\sqrt{7}}{7}$.⇒sin∠BEC=$\frac{\sqrt{21}}{7}$,
sin∠AED=sin(1200+∠BEC)=$\frac{\sqrt{3}}{2}×\frac{2\sqrt{7}}{7}-\frac{1}{2}×\frac{\sqrt{21}}{7}=\frac{\sqrt{21}}{14}$,⇒cos∠AED=$\frac{5\sqrt{7}}{14}$,
在直角△ADE中,AE=5,$\frac{AE}{DE}$═cos∠AED=$\frac{5\sqrt{7}}{14}$,⇒DE=2$\sqrt{7}$,
在△CED中,由余弦定理得CD2=CE2+DE2-2CE•DEcos120°=49
∴CD=7.
点评 本题考查了正余弦定理在解三角形中的应用,是中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<0} | B. | {x|-1<x<0} | C. | {-2,0} | D. | {x|1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“p∨q为真”是命题“p∧q为真”的必要条件 | |
| B. | 向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}•\overrightarrow{b}>0$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 | |
| C. | 若am2≤bm2,则a≤b | |
| D. | “?x0∈R,x02-x0≤0”的否定是“?x∈R,x2-x≥0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
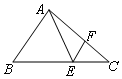 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )| A. | $\frac{{\sqrt{7}}}{14}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{14}$ | D. | $\frac{{\sqrt{21}}}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com