
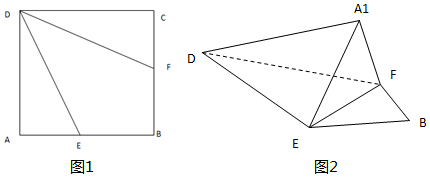
分析 (Ⅰ)折叠前有AD⊥AE,CD⊥CF,折叠后有A1D⊥A1E,A1D⊥A1F,从而A1D⊥平面A1EF,由此能证明A1D⊥EF.
(Ⅱ)取EF的中点O,连接A1O,三棱锥A1-DEF的体积${V_{{A_1}-EFD}}=\frac{1}{3}•{S_{△E{A_1}F}}•{A_1}D$,由此能求出结果.
解答 解::(Ⅰ)折叠前有AD⊥AE,CD⊥CF,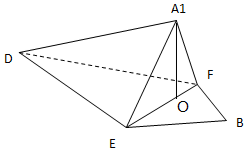
折叠后有A1D⊥A1E,A1D⊥A1F,
又A1E∩A1F=A1,∴A1D⊥平面A1EF,
∴A1D⊥EF.…(6分)
解:(Ⅱ)由正方形ABCD的边长为2,
折叠后A1D=2,${A_1}E={A_1}F=\frac{3}{2}$,$EF=\frac{{\sqrt{2}}}{2}$,
取EF的中点O,连接A1O,
则${A_1}O=\sqrt{{A_1}{E^2}-E{O^2}}=\frac{{\sqrt{34}}}{4}$
∴${S_{△E{A_1}F}}=\frac{1}{2}•{A_1}O•EF=\frac{{\sqrt{17}}}{8}$,
∴${V_{{A_1}-EFD}}=\frac{1}{3}•{S_{△E{A_1}F}}•{A_1}D=\frac{{\sqrt{17}}}{12}$.…(12分)
点评 本题考查柱、锥、台体的体积,解答此题的关键是注意折叠问题在折叠前后的变量与不变量,考查空间想象能力与计算能力,是中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
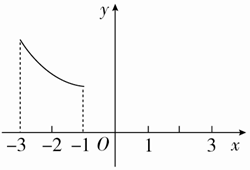 定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.
定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
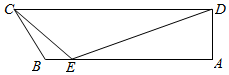 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 乙 | ||||||||||||
| 8 | 9 | 9 | 8 | 9 | 9 | 3 | 8 | 9 | 9 | ||||
| 2 | 0 | 1 | 0 | 4 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com