
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,过原点
上,过原点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
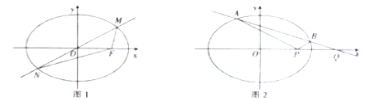
(Ⅱ)设![]() ,
,![]() ,过点
,过点![]() 且斜率不为零的直线与椭圆
且斜率不为零的直线与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,证明:
两点,证明:![]() .
.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)求出函数的导数,得到关于![]() 的方程组,解出即可;
的方程组,解出即可;
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,令
,令![]() , 利用导数研究其单调性可得
, 利用导数研究其单调性可得
![]() ,
,
从而证明![]() .
.
试题解析:((1)由题意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,则
,则![]() ,与
,与![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,
,
令![]() ,
,
![]() ,
,
令![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递减,且
单调递减,且![]() ;
;
当![]() 时,
时, ![]() ,
, ![]() 单调递增;且
单调递增;且![]() ,
,
所以![]() 在
在![]() 上当单调递减,在
上当单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
故![]() ,
,
故![]() .
.
【点睛】本题考查利用函数的切线求参数的方法,以及利用导数证明不等式的方法,解题时要认真审题,注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线方程为![]() .
.
(1)证明:直线恒过定点;
(2)![]() 为何值时,点
为何值时,点![]() 到直线的距离最大,最大值为多少?
到直线的距离最大,最大值为多少?
(3)若直线分别与![]() 轴,
轴,![]() 轴的负半轴交于
轴的负半轴交于![]() 两点,求
两点,求![]() 面积的最小值及此时直线的方程.
面积的最小值及此时直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,某公交公司分别推出支付宝和徽信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表l所示:
表1

根据以上数据,绘制了如右图所示的散点图.
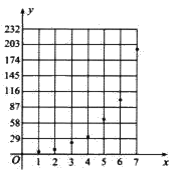
(1)根据散点图判断,在推广期内,![]() (c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次;
参考数据:

其中![]()
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: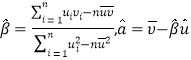 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为了测量某一隧道两侧A、B两地间的距离,某同学首先选定了不在直线AB上的一点C(![]() 中∠A、∠B、∠C所对的边分别为a、b、c),然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量∠A,∠C,b;②测量∠A,∠B,∠C;③测量a,b,∠C;④测量∠A,∠B,a,则一定能确定A、B间距离的所有方案的序号为( )
中∠A、∠B、∠C所对的边分别为a、b、c),然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量∠A,∠C,b;②测量∠A,∠B,∠C;③测量a,b,∠C;④测量∠A,∠B,a,则一定能确定A、B间距离的所有方案的序号为( )
A.①③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,
, ![]() 是集合
是集合![]() 的所有子集组成的集合.若集合
的所有子集组成的集合.若集合![]() 满足对任意的映射
满足对任意的映射![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,其中,
成立,其中,![]() 表示集合
表示集合![]() 的子集
的子集![]() 的补集,
的补集,![]() 为给定的正整数.试求所有满足上述条件的集合
为给定的正整数.试求所有满足上述条件的集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海的国家会展中心举办.国家展、企业展、经贸论坛、高新产品汇集……首届进博会高点纷呈.一个更加开放和自信的中国,正用实际行动为世界构筑共同发展平台,展现推动全球贸易与合作的中国方案.
某跨国公司带来了高端智能家居产品参展,供购商洽谈采购,并决定大量投放中国市场.已知该产品年固定研发成本30万美元,每生产一台需另投入90美元.设该公司一年内生产该产品![]() 万台且全部售完,每万台的销售收入为
万台且全部售完,每万台的销售收入为![]() 万美元,
万美元,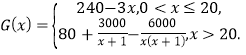
(1)写出年利润![]() (万美元)关于年产量
(万美元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com