
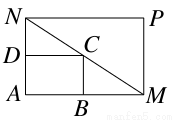
如图,已知小矩形花坛ABCD中,AB=3 m,AD=2 m,现要将小矩形花坛建成大矩形花坛AMPN,使点B在AM上,点D在AN上,且对角线MN过点C.
(1)要使矩形AMPN的面积大于32 m2,AN的长应在什么范围内?
(2)M,N是否存在这样的位置,使矩形AMPN的面积最小?若存在,求出这个最小面积及相应的AM,AN的长度;若不存在,说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-3空间点直线平面之间的位置关系(解析版) 题型:解答题
A是△BCD平面外的一点,E,F分别是BC,AD的中点.
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:填空题
观察下列等式:
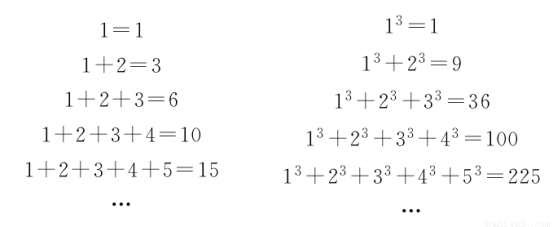
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:解答题
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).
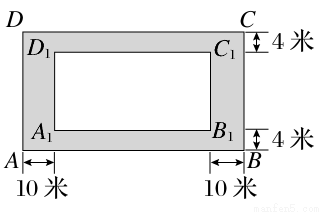
(1)若设休闲区的长和宽的比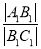 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:选择题
若a>0,b>0,且a+b=2,则ab+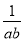 的最小值为( )
的最小值为( )
A.2 B.3 C.4 D.2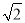
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:填空题
对于满足0≤a≤4的实数a,使x2+ax>4x+a-3恒成立的x取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:选择题
已知x>y>z,x+y+z=0,则下列不等式中成立的是( )
A.xy>yz B.xz>yz
C.xy>xz D.x|y|>z|y|
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:选择题
数列{an}的通项公式为an=(-1)n-1·(4n-3),则它的前100项之和S100等于( )
A.200 B.-200 C.400 D.-400
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com