
| 试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
分析 (Ⅰ)由$\overline{y}$=$\frac{1}{6}$$\sum_{i=1}^{6}{y}_{i}$=80,可求出q的值;
(Ⅱ)求出回归系数,可得线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\overrightarrow{a}$;
(Ⅲ)确定基本事件的个数,即可得出结论.
解答 解:(Ⅰ)由$\overline{y}$=$\frac{1}{6}$$\sum_{i=1}^{6}{y}_{i}$=80,求得q=90.
(Ⅱ)$\stackrel{∧}{b}$=$\frac{3050-6×6.5×80}{271-253.5}$=-4,$\stackrel{∧}{a}$=80+4×6.5=106,
所以所求的线性回归方程为$\stackrel{∧}{y}$=-4x+106.
(Ⅲ)当x1=4时,y1=90;当x2=5时,y2=9086;当x3=6时,y3=82;当x4=7时,y4=78;当x5=8时,y5=74;当x6=9时,y6=70.
与销售数据对比可知满足|$\stackrel{∧}{{y}_{i}}$-yi|≤1(i=1,2,…,6)的共有3个“好数据”:(4,90)、(6,8.3)、(8,7.5).
从6个销售数据中任意抽取2个的所有可能结果有$\frac{6×5}{2}$=15种,
其中2个数据中至少有一个是“好数据”的结果有3×3+3=12种,
于是从抽得2个数据中至少有一个销售数据中的产品销量不超过80的概率为$\frac{12}{15}$=$\frac{4}{5}$.
点评 本题考查线性回归方程,考查概率的计算,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | -$\frac{\sqrt{10}}{2}$ | C. | -$\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{10}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
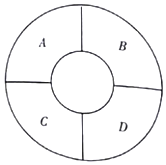 如图,一环形花坛分成A,B,C,D四块,现有3种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为( )
如图,一环形花坛分成A,B,C,D四块,现有3种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为( )| A. | 12 | B. | 24 | C. | 18 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,0) | B. | (0,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
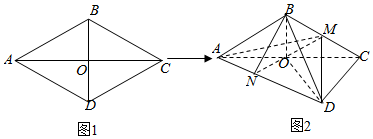
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com