
分析 (Ⅰ)求出f(x)的导数,设f(x)的图象与x轴相交于点(x0,0),可得$\left\{\begin{array}{l}f({x_0})=0\\ f'({x_0})=0\end{array}\right.$,解方程可得a=1,原不等式等价于lnx≤x-1,设h(x)=lnx-x+1,求出导数和单调区间,可得极值、最值,即可得证;
(Ⅱ)设$h(x)=\frac{x-1}{lnx}(x>1)$,求出导数,运用(Ⅰ)的结论可得h(x)单调递增,再由不等式的性质可得
$\frac{{{x^2}-1}}{{ln{x^2}}}<\frac{b-1}{lnb}$,即g(x)>0,再运用不等式的性质,证得$\frac{b-1}{lnb}<b$,进而证得右边不等式.
解答 证明:(Ⅰ)函数f(x)=a(lnx-1)+$\frac{1}{x}$的导数为$f'(x)=\frac{a}{x}-\frac{1}{x^2}$,
设f(x)的图象与x轴相交于点(x0,0),
则$\left\{\begin{array}{l}f({x_0})=0\\ f'({x_0})=0\end{array}\right.$即$\left\{\begin{array}{l}a(ln{x_0}-1)+\frac{1}{x_0}=0\\ \frac{a}{x_0}-\frac{1}{{{x_0}^2}}=0\end{array}\right.$,
解得a=x0=1.
所以$f(x)=lnx-1+\frac{1}{x}$,$f(x)≤\frac{{{{(x-1)}^2}}}{x}$等价于lnx≤x-1.
设h(x)=lnx-x+1,则$h'(x)=\frac{1}{x}-1$,
当0<x<1时,h'(x)>0,h(x)单调递增;
当x>1时,h'(x)<0,h(x)单调递减,
所以h(x)≤h(1)=0,
即lnx≤x-1,所以$f(x)≤\frac{{{{(x-1)}^2}}}{x}$.
(Ⅱ)设$h(x)=\frac{x-1}{lnx}(x>1)$,则$h'(x)=\frac{{lnx+\frac{1}{x}-1}}{{{{ln}^2}x}}$,
由(Ⅰ)可知,当x>1时,$lnx+\frac{1}{x}-1>0$,
从而有h'(x)>0,所以h(x)单调递增,
又$1<x<\sqrt{b}$,所以1<x2<b,
从而有h(x2)<h(b),即$\frac{{{x^2}-1}}{{ln{x^2}}}<\frac{b-1}{lnb}$,
所以$\frac{{{x^2}-1}}{2}<\frac{(b-1)lnx}{lnb}=(b-1){log_b}x$,
即g(x)>0,$g(x)=(b-1){log_b}x-\frac{{{x^2}-1}}{2}$=$\frac{(b-1)lnx}{lnb}-\frac{{{x^2}-1}}{2}$
=$(b-1)•\frac{{ln{x^2}}}{2lnb}-\frac{{{x^2}-1}}{2}$$<(b-1)•\frac{{{x^2}-1}}{2lnb}-\frac{{{x^2}-1}}{2}$=$\frac{{{x^2}-1}}{2}•(\frac{b-1}{lnb}-1)$,
又$lnb>1-\frac{1}{b}$,所以$\frac{b-1}{lnb}<b$,
又1<x2<b,所以$g(x)<\frac{{({x^2}-1)(b-1)}}{2}<\frac{{{{(b-1)}^2}}}{2}$.
综上可知,$0<g(x)<\frac{{{{(b-1)}^2}}}{2}$.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查转化思想和构造函数法,以及不等式的性质,考查运算求解能力,属于难题.


科目:高中数学 来源: 题型:解答题
| 试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)>0 | B. | f(x)<0 | C. | f(x)为减函数 | D. | f(x)为增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
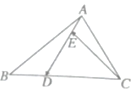 如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )
如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )| A. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{8}{9}\overrightarrow{AC}$ | B. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{8}{9}\overrightarrow{AC}$ | C. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{7}{9}\overrightarrow{AC}$ | D. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{7}{9}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{4},+∞})$ | B. | $({-\frac{1}{4},0})$ | C. | $({-\frac{1}{4},2})$ | D. | $[{-\frac{1}{4},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -10 | C. | -32 | D. | -42 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0>0,(x0,$\frac{1}{2}$)∈D | B. | ?x0>0,(x0,$\frac{1}{2}$x0)∉D | C. | ?x0>0,(x0,$\frac{1}{2}$)∈D | D. | ?x0>0,(x0,$\frac{1}{2}$x0)∉D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com