
某造纸厂拟建一座平面图形为矩形且面积为162 m2的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/m2,中间两道隔墙建造单价为248元/m2,池底建造单价为80元/m2,水池所有墙的厚度忽略不计.
(1) 试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2) 若由于地形限制,该池的长和宽都不能超过16 m,试设计污水池的长和宽,使总造价最低,并求出最低总造价.

解:(1) 设污水处理池的宽为x m,则长为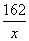 m.
m.
总造价为f(x)=400×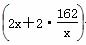 +248×2x+80×162=1 296x+
+248×2x+80×162=1 296x+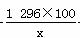 +12 960=1 296
+12 960=1 296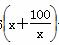 +1 2960≥1 296×2
+1 2960≥1 296×2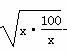 +12 960=38 880元.当且仅当x=
+12 960=38 880元.当且仅当x= (x>0),即x=10时取等号.∴ 当长为16.2 m,宽为10 m时总造价最低,最低总造价为38 880元.
(x>0),即x=10时取等号.∴ 当长为16.2 m,宽为10 m时总造价最低,最低总造价为38 880元.
(2) 由限制条件知 ∴ 10
∴ 10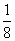 ≤x≤16.设g(x)+x+
≤x≤16.设g(x)+x+ ,由函数性质易知g(x)在
,由函数性质易知g(x)在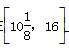 上是增函数,∴ 当x=10
上是增函数,∴ 当x=10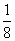 时(此时
时(此时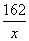 =16),g(x)有最小值,即f(x)有最小值1 296×
=16),g(x)有最小值,即f(x)有最小值1 296×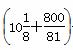 +12 960=38 882(元).∴ 当长为16 m,宽为10
+12 960=38 882(元).∴ 当长为16 m,宽为10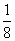 m时,总造价最低,为38 882元.
m时,总造价最低,为38 882元.


科目:高中数学 来源: 题型:
某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
科目:高中数学 来源: 题型:
下列问题属于超几何分布的有________.(填序号)
① 抛掷三枚骰子,所得向上的数是6的骰子的个数记为X,求X的概率分布列;
② 有一批种子的发芽率为70%,现任取10颗种子做发芽实验,把实验中发芽的种子的个数记为X,求X的概率分布列;
③ 一盒子中有红球3只,黄球4只,蓝球5只,现任取3只球,把不是红色的球的个数记为X,求X的概率分布列;
④ 某班级有男生25人,女生20人,现选派4名学生参加学校组织的活动,班长必须参加,其中女生人数记为X,求X的概率分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com