
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | 2 | D. | -2 |
分析 利用平面向量的数量积公式得到向量$\overrightarrow{b}$在向量$\overrightarrow{a}$上的射影为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$.
解答 解:由已知,向量$\overrightarrow{b}$在向量$\overrightarrow{a}$上的射影为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=|$\overrightarrow{b}|$cos120°=4×(-$\frac{1}{2}$)=-2;
故选D.
点评 本题考查了平没戏了的数量积的几何意义;关键是熟练运用公式.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A. | 0 | B. | 2.2 | C. | 2.6 | D. | 3.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 64 | B. | 63 | C. | 62 | D. | 61 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2011 | B. | $\frac{2011}{2}$ | C. | 22011 | D. | 2-2011 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:解答题
已知数列 是等差数列,公差
是等差数列,公差 ,
, ,
,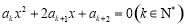 .
.
(1)求证:当 取不同正整数时,方程都有公共根;
取不同正整数时,方程都有公共根;
(2)若方程不同的根依次为 ,
, ,
,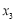 ,…,
,…, ,求证:
,求证: ,
, ,
, ,…,
,…, ,…是等差数列.
,…是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com