
分析 (1)由题意可得:$\frac{1}{2}×2cb$=$\sqrt{3}$,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,解得即可得出.
(2)设点P(x0,y0)为圆x2+y2=16上一点,PA,PB为椭圆C:$\frac{{x}^{2}}{4}$+y2=1的切线,切点A(x1,y1),B(x2,y2).
可得弦AB所在直线方程为$\frac{x{x}_{0}}{4}+y{y}_{0}$=1.可得M$(0,\frac{1}{{y}_{0}})$,N$(\frac{4}{{x}_{0}},0)$,于是|MN|2=$\frac{16}{{x}_{0}^{2}}$+$\frac{1}{{y}_{0}^{2}}$=$(\frac{16}{{x}_{0}^{2}}+\frac{1}{{y}_{0}^{2}})$×$\frac{{x}_{0}^{2}+{y}_{0}^{2}}{16}$=$\frac{1}{16}(\frac{{x}_{0}^{2}}{{y}_{0}^{2}}+\frac{16{y}_{0}^{2}}{{x}_{0}^{2}}+17)$,利用基本不等式的性质即可得出.
解答 解:(1)由题意可得:$\frac{1}{2}×2cb$=$\sqrt{3}$,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,解得a=2,b=1.
∴椭圆C方程为:$\frac{{x}^{2}}{4}$+y2=1.
(2)设点P(x0,y0)为圆x2+y2=16上一点,PA,PB为椭圆C:$\frac{{x}^{2}}{4}$+y2=1的切线,
切点A(x1,y1),B(x2,y2).
∴弦AB所在直线方程为$\frac{x{x}_{0}}{4}+y{y}_{0}$=1.
∴M$(0,\frac{1}{{y}_{0}})$,N$(\frac{4}{{x}_{0}},0)$,
∴|MN|2=$\frac{16}{{x}_{0}^{2}}$+$\frac{1}{{y}_{0}^{2}}$=$(\frac{16}{{x}_{0}^{2}}+\frac{1}{{y}_{0}^{2}})$×$\frac{{x}_{0}^{2}+{y}_{0}^{2}}{16}$=$\frac{1}{16}(\frac{{x}_{0}^{2}}{{y}_{0}^{2}}+\frac{16{y}_{0}^{2}}{{x}_{0}^{2}}+17)$≥$\frac{1}{6}(17+2\sqrt{16•\frac{{x}_{0}^{2}}{{y}_{0}^{2}}×\frac{{y}_{0}^{2}}{{x}_{0}^{2}}})$=$\frac{25}{16}$.
当且仅当${x}_{0}^{2}$=$\frac{64}{5}$,${y}_{0}^{2}$=$\frac{16}{5}$时取等号,
∴|MN|$≥\frac{5}{4}$,|MN|的最小值为$\frac{5}{4}$.
点评 本题考查了椭圆的标准方程及其性质、基本不等式的性质、椭圆的切线方程,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
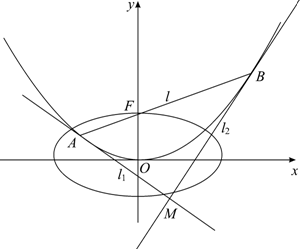 已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=$\frac{{\sqrt{3}}}{2}$.
已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
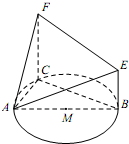 如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.
如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com