
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,命题p:任意x∈R,都有cosx≤1,则¬p:存在x0∈R,使得cosx0>1;
②,若P(ξ>4)=P(ξ<2)成立,正态曲线关于直线x=3对称;当P(ξ≤0)=0.2时,则P(0<ξ<6)=0.6,
③,若$\overrightarrow{OA}=3\overrightarrow{OB}=2\overrightarrow{OC}$,则A,B,C三点共线,若A,B,C三点共线时,$\overrightarrow{OA}=3\overrightarrow{OB}=2\overrightarrow{OC}$不一定成立,
④,线性回归方程y=bx+a对应的直线一定经过其散点图中心.
解答 解:对于①,命题p:任意x∈R,都有cosx≤1,则?p:存在x0∈R,使得cosx0>1;故错
对于②,若P(ξ>4)=P(ξ<2)成立,正态曲线关于直线x=3对称;当P(ξ≤0)=0.2时,则P(0<ξ<6)=0.6,故错
对于③,若$\overrightarrow{OA}=3\overrightarrow{OB}=2\overrightarrow{OC}$,则A,B,C三点共线,若A,B,C三点共线时,$\overrightarrow{OA}=3\overrightarrow{OB}=2\overrightarrow{OC}$不一定成立,故正确;
对于④,线性回归方程y=bx+a对应的直线不一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个,故错.
故选:A
点评 本题考查了命题真假判定,含有量词的特称命题、充要条件、线性回归等基础知识,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{3}$ | B. | $2\sqrt{7}$ | C. | $\frac{20}{3}$ | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
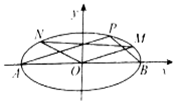 如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.
如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
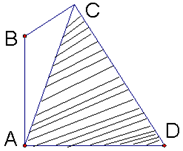 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com