
分析 利用已知条件求出等差数列的前n项和,然后化简所求的表达式,求解即可.
解答 解:等差数列{an}的前n项和为Sn,a3=3,S4=10,S4=2(a2+a3)=10,
可得a2=2,数列的首项为1,公差为1,
Sn=$\frac{n(n+1)}{2}$,$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$,
则 $\sum_{k=1}^{n}$$\frac{1}{{S}_{k}}$=2[1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$]=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$.
故答案为:$\frac{2n}{n+1}$.
点评 本题考查等差数列的求和,裂项消项法求和的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
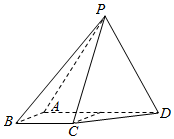 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
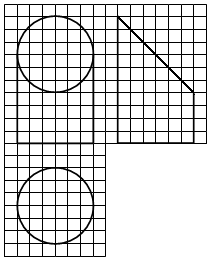 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )| A. | 90π | B. | 63π | C. | 42π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com