Question

4．已知抛物线C：y²=2px（p＞0），O为坐标原点，过点M（2p，0）作直线l交抛物线于A、B两点．有如下命题：
①|$\overrightarrow{OA}{|^2}+|\overrightarrow{OB}{|^2}=|\overrightarrow{AB}{|^2}$
②|$\overrightarrow{AB}$|≥4p
③（S_△OAB）_min=4p²
④△OAB周长的最小值为$4（1+\sqrt{2}）p$
则上述命题正确的是（　　）

• A． ①②
• B． ①②③
• C． ②③④
• D． ①②③④

Answer 1

分析 如图所示，设A（x₁，y₁），B（x₂，y₂），设直线AB的方程为：x=my+2p，与抛物线方程联立可得y²-2pmy-4p²=0，利用根与系数的关系可得：$\overrightarrow{OA}•\overrightarrow{OB}$=x₁x₂+y₁y₂=0，得到OA⊥OB，|$\overrightarrow{OA}{|^2}+|\overrightarrow{OB}{|^2}=|\overrightarrow{AB}{|^2}$，可知①正确；利用弦长公式可得$|\overrightarrow{AB}|$=$\sqrt{（1+{m}^{2}）[（{y}_{1}+{y}_{2}）^{2}-4y{y}_{1}{y}_{2}]}$=$\sqrt{（1+{m}^{2}）[4{p}^{2}{m}^{2}+16{p}^{2}]}$，可知②正确
原点O到直线AB的距离h=$\frac{2p}{\sqrt{1+{m}^{2}}}$．利用S_△OAB=$\frac{1}{2}h•|AB|$，即可判断出面积最小值；利用|OA|+|OB|≥$2\sqrt{|OA||OB|}$≥$2\sqrt{8{p}^{2}}$=$4\sqrt{2}$p，及其②即可判断出④的正误．

解答 解：如图所示，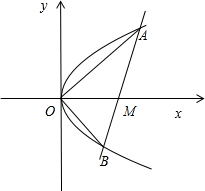
设A（x₁，y₁），B（x₂，y₂），
设直线AB的方程为：x=my+2p，
联立$\left\{\begin{array}{l}{x=my+2p}\\{{y}^{2}=2px}\end{array}\right.$，
∴y²-2pmy-4p²=0，
∴y₁+y₂=2pm，y₁y₂=-4p²，
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x₁x₂+y₁y₂=（my₁+2p）（my₂+2p）+y₁y₂=（m²+1）y₁y₂+2pm（y₁+y₂）+4p²=-4p²（1+m²）+4p²m²+4p²=0，
∴OA⊥OB，∴|$\overrightarrow{OA}{|^2}+|\overrightarrow{OB}{|^2}=|\overrightarrow{AB}{|^2}$；
∴$|\overrightarrow{AB}|$=$\sqrt{（1+{m}^{2}）[（{y}_{1}+{y}_{2}）^{2}-4y{y}_{1}{y}_{2}]}$=$\sqrt{（1+{m}^{2}）[4{p}^{2}{m}^{2}+16{p}^{2}]}$≥4p，当且仅当m=0时取等号．
原点O到直线AB的距离h=$\frac{2p}{\sqrt{1+{m}^{2}}}$．
∴S_△OAB=$\frac{1}{2}h•|AB|$=$\frac{1}{2}×\frac{2p}{\sqrt{1+{m}^{2}}}$×$\sqrt{（1+{m}^{2}）[4{p}^{2}{m}^{2}+16{p}^{2}]}$≥4p²，当且仅当m=0时取等号．
∵|OA|+|OB|≥$2\sqrt{|OA||OB|}$≥$2\sqrt{8{p}^{2}}$=$4\sqrt{2}$p，
∴△OAB周长=|OA|+|OB|+|AB|≥$4（1+\sqrt{2}）p$．
综上可知：①②③④都正确．
故选：D．

点评 本题考查了直线与抛物线相交问题转化为方程联立可得根与系数的关系、弦长公式、面积计算公式、基本不等式的性质、点到直线的距离公式，考查了推理能力与计算能力，属于难题．