练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．求证：函数f（x）=$\sqrt{x}$+a在（0，+∞）上是增函数．

    分析 根据函数单调性的定义证明即可．

    解答 证明：设?x1，x2满足x1＞x2＞0，
    则f（x1）-f（x2）=$\sqrt{{x}_{1}}$-$\sqrt{{x}_{2}}$=$\frac{（\sqrt{{x}_{1}}-\sqrt{{x}_{2}}）（\sqrt{{x}_{1}}+\sqrt{{x}_{2}}）}{\sqrt{{x}_{1}}+\sqrt{{x}_{2}}}$=$\frac{{x}_{1}{-x}_{2}}{\sqrt{{x}_{1}}+\sqrt{{x}_{2}}}$，
    ∵$\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$＞0，x1-x2＞0，∴f（x1）-f（x2）＞0，
    ∴f（x）=$\sqrt{x}$+a在（0，+∞）上是增函数．

    点评 本题考查了根据函数的单调性的定义证明函数的单调性问题，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．已知集合A={x|x＜0}，B={x|（x+2）（x-3）≤0}，则A∩B=（　　）
    A．{x|-3≤x＜0}B．{x|-3＜x＜-2}C．{x|-2≤x＜0}D．{x|x≤3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知（4$\root{4}{\frac{1}{x}}$+$\root{3}{{x}^{2}}$）n展开式中的倒数第三项的二项式系数为45．
    （1）求n；
    （2）求含有x3的项；
    （3）求二项式系数最大的项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

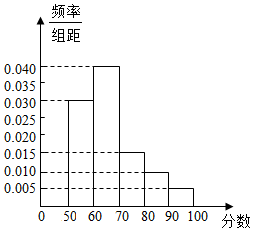    4．某校举行的数学知识竞赛中，将参赛学生的成绩在进行整理后分成5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组．已知第三小组的频数是15．
    （1）求成绩在50-70分的频率是多少；
    （2）求这次参赛学生的总人数是多少；
    （3）求这次数学竞赛成绩的平均分的近似值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．求函数y=2+2sinxcosx+sinx+cosx的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．不等式x2+x＜$\frac{a}{b}$+$\frac{b}{a}$ 对任意a，b∈（0，+∞）恒成立，则实数x的取值范围是（　　）
    A．（-2，0）B．（-∞，-2）∪（1，+∞）C．（-2，1）D．（-∞，-4）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知数列{an}的通项公式an=n22n，则数列{an}的前n项和Sn=（n2-2n+3）•2n+1-6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=2$\sqrt{3}$sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$-2sin2$\frac{ωx}{2}$（ω＞0）的最小正周期为3π．
    （I）求函数f（x）的单调递增区间；
    （Ⅱ）在△ABC中，a，b，c分别为角A，B，C所对的边，a＜b＜c，$\sqrt{3}$a=2csinA，并且f（$\frac{3}{2}$A+$\frac{π}{2}$）=$\frac{11}{13}$，求cosB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在△ABC中，a，b，c分别为内角A，B，C的对边，且$\frac{cosA-3cosC}{cosB}=\frac{3c-a}{b}$．
    （1）求$\frac{sinC}{sinA}$的值；
    （2）若B为钝角，b=10，求a的取值范围．

    查看答案和解析>>

    同步练习册答案