Question

8．在△ABC中，a=15，b=10，A=60°，CE、CF三等分∠C，求CE、CF的长．

Answer 1

分析 利用正弦定理可求sinB，结合大边对大角可得B为锐角，可得B=35.26°，进而可求C，设三等分角为x，则x=28.25°，在△BEC中，由正弦定理可求CE，在△ACF中，正弦定理可求FC的值．

解答 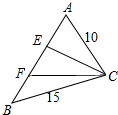解：∵a=15，b=10，A=60°，
∴sinB=$\frac{bsinA}{a}$=$\frac{10×\frac{\sqrt{3}}{2}}{15}$=$\frac{\sqrt{3}}{3}$．
∴b＜a，可得：B为锐角，B=35.26°，
∴C=180°-A-B=84.74°，
∴由CE、CF三等分∠C，设三等分角为x，则x=28.25°，
在△BEC中，正弦定理$\frac{CE}{sinB}=\frac{a}{sin（180°-B-2x）}$，可得：CE=$\frac{asinB}{sin（180°-B-2x）}$=$\frac{15×sin35.26°}{sin116.24°}$=9.65．
在△ACF中，正弦定理$\frac{FC}{sinA}=\frac{b}{sin（180°-A-2x）}$，可得：FC=$\frac{bsinA}{sin（180°-A-2x）}$=$\frac{10×sin60°}{sin91.75°}=8.66$

点评 本题主要考查了正弦定理在解三角形中的应用，考查了计算能力和转化思想，属于中档题．