
| A. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) | B. | (-$\sqrt{2}$,-1)∪(1,$\sqrt{2}$) | C. | (-5,-$\sqrt{2}$)∪($\sqrt{2}$,6) | D. | (-∞,-6)∪(6,+∞) |
分析 原方程等价于x3+m=$\frac{2}{x}$,原方程的实根是曲线y=x3+m与曲线y=$\frac{2}{x}$的交点的横坐标,分别作出左右两边函数的图象:分m>0与m<0讨论,可得答案
解答 
 解:∵集合A={x∈R|x4+mx-2=0},
解:∵集合A={x∈R|x4+mx-2=0},
∴方程的根显然x≠0,原方程等价于x3+m=$\frac{2}{x}$,
原方程的实根是曲线y=x3+m与曲线y=$\frac{2}{x}$的交点的横坐标,
而曲线y=x3+m是由曲线y=x3向上或向下平移|m|个单位而得到的,
若交点(x1,$\frac{2}{{x}_{1}}$)(i=1,2,…,k)均在直线y=x的同侧,
因直线y=x与y=$\frac{2}{x}$交点为:(-$\sqrt{2}$,-$\sqrt{2}$),($\sqrt{2}$,$\sqrt{2}$);
所以结合图象可得$\left\{\begin{array}{l}{m>0}\\{(-\sqrt{2})^{3}+m>-\sqrt{2}}\\{x<-\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m<0}\\{(\sqrt{2})^{3}+m<\sqrt{2}}\\{x>\sqrt{2}}\end{array}\right.$,
解得m>$\sqrt{2}$或m<-$\sqrt{2}$.
答案为:m>$\sqrt{2}$或m<-$\sqrt{2}$.
故选:A.
点评 本题综合考查了反比例函数,反比例函数与一次函数图象的交点问题,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABC-A1B1C1中,AB>A1B1,给出如下两个命题:命题甲:AB∥A1B1,BC∥B1C1;命题乙:多面体ABC-A1B1C1是棱台.试问:从命题甲能否推出命题乙?反之,结果如何?
如图,在多面体ABC-A1B1C1中,AB>A1B1,给出如下两个命题:命题甲:AB∥A1B1,BC∥B1C1;命题乙:多面体ABC-A1B1C1是棱台.试问:从命题甲能否推出命题乙?反之,结果如何?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
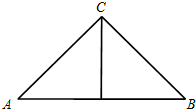 如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )
如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 9 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | m | 5 | |
| 女生 | 10 | n | |
| 合计 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com