Question

【题目】已知函数.

（1）求的单调减区间；

（2）当在区间上变化时，求的极小值的最大值.

Answer 1

【答案】（1）若，的单调递减区间为；若， 的单调递减区间为，；当时， ，单调递减；当时，函数无单调减区间；⑤当时，单调递减；（2）.

【解析】

（1）当时，代入解析式，结合二次函数性质即可求得其单调递减区间；当时，两个零点相等，因而将两个的值代入判断，并分、和三段讨论，解不等式即可得的单调递减区间；

（2）根据导函数的符号，判断的单掉区间，并表示出其极小值.结合二次函数性质即可求得的极小值的最大值.

（1）函数.

①若，，

则的单调递减区间为；

②若，则.

令，得，即或.

则的单调递减区间为，；

③当时，令，可解得递减区间为，;

④当时，代入可知无解，所以函数无单调减区间，

⑤，令，解不等式可得单调递减递减区间为时.

（2），.

当时，，单调递增，

当时，，单调递减，

当时，，单调递增，

∴的极小值为

，

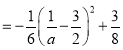当时，函数的极小值取得最大值为.