
分析 对判别式△进行讨论,结合二次函数的图象性质列出不等式组解出.
解答 解:令f(x)=2x2-3x+2m=0,得m=-x2+$\frac{3x}{2}$,令g(x)=-x2+$\frac{3x}{2}$,则g(x)在(-1,$\frac{3}{4}$]上单调递增,在($\frac{3}{4}$,1)上单调递减,
g(-1)=-$\frac{5}{2}$,g(1)=$\frac{1}{2}$,g($\frac{3}{4}$)=$\frac{9}{16}$.
作出g(x)的函数图象如图: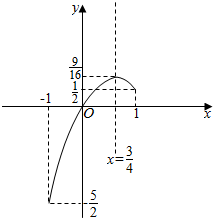
∵f(x)=2x2-3x+2m的图象与x轴在(-1,1)内仅有一个公共点,
∴m=g(x)在(-1,1)上只有一解,
由g(x)的函数图象可知-$\frac{5}{2}$$<m<\frac{1}{2}$或m=$\frac{9}{16}$.
∴m的取值范围是(-$\frac{5}{2}$,$\frac{1}{2}$)∪{$\frac{9}{16}$}.
点评 本题考查了二次函数的性质,零点的个数与系数的关系,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
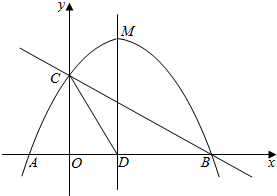 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
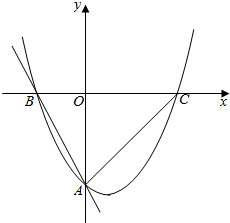 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
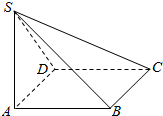 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
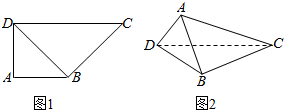 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com