练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若{an}是正项递增等比数列，Tn表示其前n项之积，且T4＝T8，则当Tn取最小值时，n的值为________．

     

    6

    【解析】由T4＝T8知，a5·a6·a7·a8＝1，则(a6·a7)2＝1，∵{an}为正项递增等比数列，∴a6·a7＝1且a6<1，a7>1，故Tn取最小值时，n的值为6.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：填空题

    若a，b，c>0，且a2＋ab＋ac＋bc＝4，则2a＋b＋c的最小值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-5数列的综合应用（解析版） 题型：解答题

    某企业为加大对新产品的推销力度，决定从今年起每年投入100万元进行广告宣传，以增加新产品的销售收入．已知今年的销售收入为250万元，经市场调查，预测第n年与第n－1年销售收入an与an－1(单位：万元)满足关系式：an＝an－1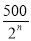＋－100.

    (1)设今年为第1年，求第n年的销售收入an；

    (2)依上述预测，该企业前几年的销售收入总和Sn最大．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-4数列求和（解析版） 题型：解答题

    已知各项均不相等的等差数列{an}的前n项和为Sn，若S3＝15，且a3＋1为a1＋1和a7＋1的等比中项．

    (1)求数列{an}的通项公式与前n项和Sn；

    (2)设Tn为数列{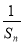}的前n项和，问是否存在常数m，使Tn＝m[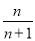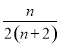＋]，若存在，求m的值；若不存在，说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-4数列求和（解析版） 题型：选择题

    数列1,1＋2,1＋2＋4，…，1＋2＋22＋…＋2n－1，…的前n项和Sn>1020，那么n的最小值是(　　)

    A．7 B．8 C．9 D．10

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-3等比数列及其前n项和（解析版） 题型：选择题

    已知正项等比数列{an}满足：a7＝a6＋2a5，若存在两项am，an使得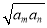＝4a1，则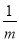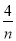＋的最小值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-2等差数列及其前n项和（解析版） 题型：填空题

    已知数列{an}中a1＝1，a2＝2，当整数n>1时，Sn＋1＋Sn－1＝2(Sn＋S1)都成立，则S15＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-1数列的概念与简单表示法（解析版） 题型：选择题

    一函数y＝f(x)的图象在给定的下列图象中，并且对任意an∈(0,1)，由关系式an＋1＝f(an)得到的数列{an}满足an＋1>an(n∈N*)，则该函数的图象是(　　)

     

     

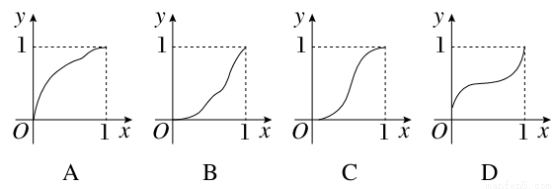
    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-3平面向量的数量积及应用（解析版） 题型：选择题

    已知平行四边形ABCD中，AC为一条对角线，若＝(2,4)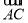，＝(1,3)，则·＝(　　)

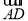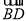    A．－8 B．－6 C．6 D．8

     

    查看答案和解析>>

    同步练习册答案