
分析 (1)由acosB=3,bcosA=l,利用余弦定理化为:a2+c2-b2=6c,b2+c2-a2=2c.相加即可得出c.
(2)由(1)可得:a2-b2=8.由正弦定理可得:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{4}{sinC}$,又A-B=$\frac{π}{6}$,可得A=B+$\frac{π}{6}$,C=$π-(2B+\frac{π}{6})$,可得sinC=sin$(2B+\frac{π}{6})$.代入可得$16si{n}^{2}(B+\frac{π}{6})$-16sin2B=$8si{n}^{2}(2B+\frac{π}{6})$,化简即可得出.
解答 解:(1)∵acosB=3,bcosA=l,∴a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=3,b×$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=1,
化为:a2+c2-b2=6c,b2+c2-a2=2c.
相加可得:2c2=8c,解得c=4.
另解:∵在△ABC中,A+B+C=π,则sinAcosB+sinBcosA=sin(A+B)=sin(π-C)=sinC,
由正弦定理得,c=acosB+bcosA=3+1=4.
(2)由(1)可得:a2-b2=8.
由正弦定理可得:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{4}{sinC}$,
又A-B=$\frac{π}{6}$,∴A=B+$\frac{π}{6}$,C=π-(A+B)=$π-(2B+\frac{π}{6})$,可得sinC=sin$(2B+\frac{π}{6})$.
∴a=$\frac{4sin(B+\frac{π}{6})}{sin(2B+\frac{π}{6})}$,b=$\frac{4sinB}{sin(2B+\frac{π}{6})}$.
∴$16si{n}^{2}(B+\frac{π}{6})$-16sin2B=$8si{n}^{2}(2B+\frac{π}{6})$,
∴1-$cos(2B+\frac{π}{3})$-(1-cos2B)=$si{n}^{2}(2B+\frac{π}{6})$,即cos2B-$cos(2B+\frac{π}{3})$=$si{n}^{2}(2B+\frac{π}{6})$,
∴-2$sin(2B+\frac{π}{6})$$sin(-\frac{π}{6})$═$si{n}^{2}(2B+\frac{π}{6})$,
∴$sin(2B+\frac{π}{6})$=0或$sin(2B+\frac{π}{6})$=1,B∈$(0,\frac{5π}{12})$.
解得:B=$\frac{π}{6}$.
另解:由正弦定理得$\frac{acosB}{bcosA}$=$\frac{sinAcosB}{sinBcosA}$=$\frac{tanA}{tanB}$=3,
又tan(A-B)=$\frac{tanA-tanB}{1+tanAatnB}$=$\frac{2tanB}{1+ta{n}^{2}B}$=$\frac{\sqrt{3}}{3}$,
解得tanB=$\frac{\sqrt{3}}{3}$,B∈(0,π),B=$\frac{π}{6}$.
点评 本题考查了正弦定理余弦定理、倍角公式、诱导公式、和差公式、三角函数求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 16 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
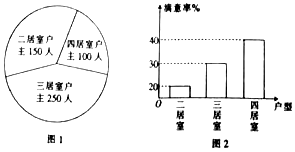 已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )| A. | 100,8 | B. | 80,20 | C. | 100,20 | D. | 80,8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,-1) | B. | ($\frac{π}{3}$,-1) | C. | ($\frac{π}{6}$,0) | D. | ($\frac{π}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | [1,2] | C. | (2,4] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={log_2}{2^{-x}}$ | B. | $y={({\frac{1}{2}})^{-x}}$ | C. | $y=\frac{1}{x+1}$ | D. | y=x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com