
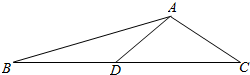
 在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD
在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD分析 (1)由题意可得D为BC中点,延长AD至E使DE=AD,连接BE、CE,则四边形ABEC为平行四边形,可得BE=AC=2,由正弦定理可得∠AEB=90°,再由勾股定理和余弦定理可得;
(2)在△ABD中由余弦定理可得cosB,进而由同角三角函数基本关系可得tanB,由两角和的正切公式可得.
解答 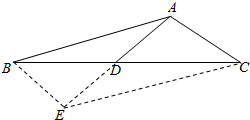 解:(1)由题意可得D为BC中点,延长AD至E使DE=AD,
解:(1)由题意可得D为BC中点,延长AD至E使DE=AD,
连接BE、CE,则四边形ABEC为平行四边形,BE=AC=2,
在△ABE中,由正弦定理可得sin∠AEB=$\frac{ABsin30°}{BE}$=1,
∴∠AEB=90°,由勾股定理可得AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=2$\sqrt{3}$,
∴在△ABD中由余弦定理可得BD2=42+($\sqrt{3}$)2-2×4×$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=7,
∴BC=BD=2$\sqrt{7}$;
(2)在△ABD中由余弦定理可得cosB=$\frac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2•AB•BD}$=$\frac{5\sqrt{7}}{14}$,
由同角三角函数基本关系可得tanB=$\frac{\sqrt{3}}{5}$,
∴tan(B+60°)=$\frac{tanB+\sqrt{3}}{1-\sqrt{3}tanB}$=3$\sqrt{3}$.
点评 本题考查两角和与差的正切函数,涉及正余弦的应用,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
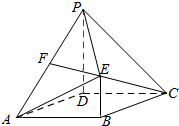 如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.
如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com