
分析 (Ⅰ)由已知得椭圆的离心率为$\frac{1}{2}$,设椭圆的方程为$\frac{x^2}{a^2}+\frac{{4{y^2}}}{{3{a^2}}}=1$,推导出a2=4,由此能求出椭圆的标准方程.
(Ⅱ)设直线为y=kx+2,联立直线l1和椭圆方程,得(3+4k2)x2+16kx+4=0,由此利用韦达定理、圆的直径的性质、向量垂直性质,能求出直线方程.(Ⅲ)由方程组$\left\{\begin{array}{l}x=ty+1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3t2+4)y2+6ty-9=0,由此利用韦达定理、弦长公式、三角形面积公式能推导出不存在直线l满足题意.
解答 (本小题满分13分)
解:(Ⅰ)双曲线${x^2}-\frac{y^2}{3}=1$的离心率为2
∴椭圆的离心率为$\frac{1}{2}$
设椭圆的长半轴为a,短半轴为b,半焦距为c,b2=a2-c2,
∴$\frac{c}{a}=\frac{1}{2}$,∴$b=\frac{{\sqrt{3}}}{2}a$,
设椭圆的方程为$\frac{x^2}{a^2}+\frac{{4{y^2}}}{{3{a^2}}}=1$
椭圆过$(\sqrt{3},-\frac{{\sqrt{3}}}{2})$点,∴$\frac{3}{a^2}+\frac{{4×\frac{3}{4}}}{{3{a^2}}}=1$,解得a2=4,
∴椭圆的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(Ⅱ)直线l1斜率必存在,且纵截距为2,设直线为y=kx+2
联立直线l1和椭圆方程$\left\{\begin{array}{l}y=kx+2\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得:(3+4k2)x2+16kx+4=0,
由△>0,得${k^2}>\frac{1}{4}$(*)
设P(x1,y1),Q(x2,y2)
则${x_1}+{x_2}=-\frac{16k}{{3+4{k^2}}},{x_1}{x_2}=\frac{4}{{3+4{k^2}}}$(1)
∵以PQ直径的圆恰过原点,∴OP⊥OQ,$\overrightarrow{OP}•\overrightarrow{OQ}=0$,
即x1x2+y1y2=0,也即x1x2+(kx1+2)(kx2+2)=0,
即(1+k2)x1x2+2k(x1+x2)+4=0,
将(1)式代入,得$\frac{{4(1+{k^2})}}{{3+4{k^2}}}-\frac{32k}{{3+4{k^2}}}+4=0$,
即4(1+k2)-32k2+4(3+4k2)=0,
解得${k^2}=\frac{4}{3}$,满足(*)式,∴$k=±\frac{{2\sqrt{3}}}{3}$.…(8分)
(Ⅲ)由方程组$\left\{\begin{array}{l}x=ty+1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3t2+4)y2+6ty-9=0(*),
设A(x1,y1),B(x2,y2),则${y_1}+{y_2}=-\frac{6t}{{3{t^2}+4}},{y_1}•{y_2}=-\frac{9}{{3{t^2}+4}}<0$,
∴$|{{y_1}-{y_2}}|=\sqrt{{{({{y_1}+{y_2}})}^2}-4{y_1}{y_2}}=\sqrt{{{(-\frac{6t}{{3{t^2}+4}})}^2}-4(-\frac{9}{{3{t^2}+4}})}=\frac{{12\sqrt{{t^2}+1}}}{{3{t^2}+4}}$,
∵直线l:x=ty+1过点F(1,0),
∴△ABE的面积${S_{△ABE}}=\frac{1}{2}|{EF}|•|{{y_1}-{y_2}}|=\frac{1}{2}×2×\frac{{12\sqrt{{t^2}+1}}}{{3{t^2}+4}}=\frac{{12\sqrt{{t^2}+1}}}{{3{t^2}+4}}$$令\frac{{12\sqrt{{t^2}+1}}}{{3{t^2}+4}}=2\sqrt{3}$,
则${t^2}=-\frac{2}{3}$不成立,故不存在直线l满足题意.…(13分)
点评 本题考查椭圆方程、直线方程的求法,是中档题,解题时要认真审题,注意韦达定理、弦长公式、三角形面积公式、椭圆性质、直线和椭圆位置关系的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
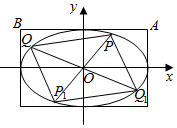 (重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$
(重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
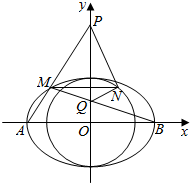 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})过点({2,\sqrt{2}})$,其焦点在⊙O:x2+y2=4上,A,B是椭圆的左右顶点.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})过点({2,\sqrt{2}})$,其焦点在⊙O:x2+y2=4上,A,B是椭圆的左右顶点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
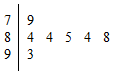 如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,2.4 | D. | 85,1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
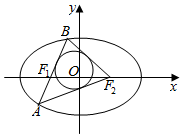 如图,设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若以△ABF2的内切圆的面积为π,设A(x1,y1)、B((x2,y2),则|y1-y2|值为$\frac{10}{3}$.
如图,设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若以△ABF2的内切圆的面积为π,设A(x1,y1)、B((x2,y2),则|y1-y2|值为$\frac{10}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com