
分析 ①根据特例a-a=0,$\frac{a}{a}$=1,可得证;
②特例一定有1+1=2,1+2=3,推下去必然包含整数集,故得证;
③根据数域的定义证明对加,减,乘,除封闭即可.
解答 证明:①数集P有两个元素a,b,则一定有a-a=0,$\frac{a}{a}$=1,故数域必含有0与1两个数,故(1)得证;
(2)数域有1,一定有1+1=2,1+2=3,推下去必然包含整数集,因而为无限集,(2)得证;
(3)当b=0是,数集A=Q,当b≠0时,数集A表示所有含$\sqrt{2}$的同类二次根式,可知,从A中任取m,n,都有其和,差,积,商仍然在集合A中,根据定义可得数集A为数域即复数集.
点评 对新型定义的考查,应紧扣定义,从定义入手.


科目:高中数学 来源: 题型:解答题
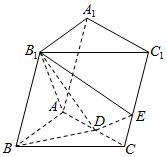 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 90° | C. | 180° | D. | 270° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com