考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)由导数的运算法则可得f′(x)=12x
2+2ax+b,由于函数f(x)=4x
3+ax
2+bx+5在x=
与x=-1时有极值,可得
,解得即可.
(2)分别解出f′(x)>0,f′(x)<0,列出表格即可得出;
(3)利用(2)可得函数f(x)在
[-1,)上单调递减,在
(,2]上单调递增.分别计算出极值与区间端点的函数值比较即可得出.
解答:
解:(1)f′(x)=12x
2+2ax+b,
∵函数f(x)=4x
3+ax
2+bx+5在x=
与x=-1时有极值;
∴
,即
,解得
.
∴f(x)=4x
3-3x
2-18x+5.
(2)由(1)可得f′(x)=12x
2-6x-18=6(x+1)(2x-3).
令f′(x)=0,解得x=-1或
.
列表如下:
| x |
(-∞,-1) |
-1 |
(-1,) |
|
(,+∞) |
| f′(x) |
+ |
0 |
- |
0 |
+ |
| f(x) |
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
由表格可得:函数f(x)的单调递增区间为(-∞,-1),
(,+∞);单调递减区间为
(-1,).
(3)由(2)可知:函数f(x)在
[-1,)上单调递减,在
(,2]上单调递增.
因此当x=
时,函数f(x)取得最小值,且
f()=-13.又f(-1)=16,f(2)=-11,∴函数f(x)的最大值为f(-1),即16.
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力和计算能力,属于中档题.



 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案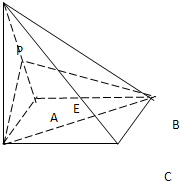 已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,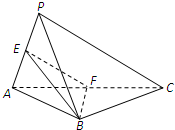 如图,在三棱锥P-ABC中,平面ABC⊥平面PAC,AB=BC,E,F分别是PA,AC的中点.求证:
如图,在三棱锥P-ABC中,平面ABC⊥平面PAC,AB=BC,E,F分别是PA,AC的中点.求证: