
分析 推导出d<0,-$\frac{29}{2}d$<a1<-15d,Sn=$\frac{d}{2}$(n+$\frac{2{a}_{1}-d}{2d}$)2+$\frac{4{{a}_{1}}^{2}-{d}^{2}+4{a}_{1}d}{8d}$.由此能求出n=15时,等差数列{an}的前n项和Sn取最大值.
解答 解:∵等差数列{an},其前n项和为Sn,且S30>0,S31<0,
∴$\left\{\begin{array}{l}{30{a}_{1}+\frac{30×29}{2}d>0}\\{31{a}_{1}+\frac{31×30}{2}d<0}\end{array}\right.$,
∴d<0,-$\frac{29}{2}d$<a1<-15d,
∴Sn=na1+$\frac{n(n-1)}{2}d$=$\frac{{n}^{2}d}{2}$+na1-$\frac{nd}{2}$
=$\frac{d}{2}$(n2+$\frac{2{a}_{1}}{d}$n-n)
=$\frac{d}{2}$(n+$\frac{2{a}_{1}-d}{2d}$)2+$\frac{4{{a}_{1}}^{2}-{d}^{2}+4{a}_{1}d}{8d}$.
∵-$\frac{29}{2}d$<a1<-15d,
∴-$\frac{29}{2}<\frac{2{a}_{1}-d}{2d}<-15$,
∴n=15时,等差数列{an}的前n项和Sn取最大值.
故答案为:15.
点评 本题考查等差数列的前n项和取最大值时项数n的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 6 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
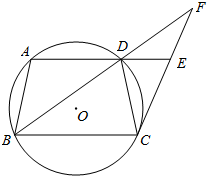 如图,梯形ABCD内接于圆O,AD∥BC,过点C作圆O的切线,交BD的延长线于点F,交AD的延长线于点E.
如图,梯形ABCD内接于圆O,AD∥BC,过点C作圆O的切线,交BD的延长线于点F,交AD的延长线于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com