
| A. | [-$\frac{1}{2}$,1] | B. | [-$\frac{1}{2}$,2] | C. | [-$\frac{1}{2}$,2) | D. | (-$\frac{1}{2}$,1) |
分析 利用分离常数法,转化为二次函数值域问题求解即可.
解答 解:函数f(x)=$\frac{2{x}^{2}-1}{{x}^{2}+2}$=$\frac{2({x}^{2}+2)-5}{{x}^{2}+2}$=$2-\frac{5}{{x}^{2}+2}$.
∵$\frac{5}{{x}^{2}+2}$∈(0,$\frac{5}{2}$]
∴-$\frac{5}{{x}^{2}+2}$∈[-$\frac{5}{2}$,0)
故得f(x)∈[-$\frac{1}{2}$,2),即函数f(x)=$\frac{2{x}^{2}-1}{{x}^{2}+2}$的值域为[-$\frac{1}{2}$,2).
故选C.
点评 本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{3\sqrt{5}}}{10}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
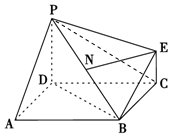 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com