练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．下列有关命题的说法正确的是（　　）
    A．p是q的必要不充分条件，则￢p是￢q的充分不必要条件
    B．对于命题p：?x∈R，使得x+x-1＜0，则￢p：?x∈R，均有x2+x-1＞0
    C．线性回归方程y=$\stackrel{∧}{b}$x+a对应的直线一定经过其样本数据点（x 1，y1）、（x2，y2）、…，（xn，yn） 中的一个
    D．“m=-1”是“直线l1：mx+（2m-1）y+1=0与直线l2：3x+my+3=0垂直”的充要条件

    分析 对四个命题分别进行判断，即可得出结论．

    解答 解：对于A，∵p是q的必要不充分条件，∴由q可以推出p成立，而由p推不出q成立，∵原命题与逆否命题是等价命题，∴由￢p可以推出￢q成立，由￢q推不出￢p成立．因此，￢p是￢q的充分不必要条件，故正确；
    对于B，对于命题p：?x∈R，使得x+x-1＜0，则￢p：?x∈R，均有x2+x-1≥0，故B错误；
    对于C，线性回归方程y=$\stackrel{∧}{b}$x+a对应的直线一定经过样本中心点，故C错误；
    对于D，直线l1：mx+（2m-1）y+1=0与直线l2：3x+my+3=0垂直，则3m+m（2m-1）=0，∴m=0或m=-1，故D不正确．
    故选：A．

    点评 本题考查了命题的判断，融合了充分必要条件的定义，线性回归方程，逻辑连接词等问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．执行如图的程序框图，当k的值为2015时，则输出的S值为（　　）
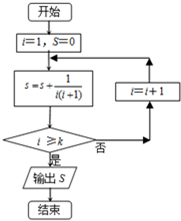
    A．$\frac{2013}{2014}$B．$\frac{2014}{2015}$C．$\frac{2015}{2016}$D．$\frac{2016}{2017}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．不等式3x＞2的解为x＞log32．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．对于自然数N*的每一个非空子集，我们定义“交替和”如下：把子集中的元素从大到小的顺序排列，然后从最大的数开始交替地加减各数，例如{1，2，4，6，9}的交替和是9-6+4-2+1=6；则集合{1，2，3，4，5，6，7}的所有非空子集的交替和的总和为448．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知角α，β满足$\frac{tanα}{tanβ}$=$\frac{7}{13}$，若sin（α+β）=$\frac{2}{3}$，则sin（α-β）的值为-$\frac{1}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．有下列叙述：
    ①“x=y”的反设是“x＞y或x＜y”；　
    ②“a＞b”的反设是“a＜b”；
    ③“三角形的外心在三角形外”的反设是“三角形的外心在三角形内”；
    ④“三角形最多有一个钝角”的反面是“三角形没有钝角”．
    其中正确的叙述有①．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．过定点（2a，0）和椭圆$\left\{\begin{array}{l}{x=acosθ}\\{y=bsinθ}\end{array}\right.$（θ为参数）上各点连线的中点轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知ω=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i．
    （1）求ω2及ω2+ω+1的值；
    （2）类比写出关于ω的其他运算性质（至少两条）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）=x${\;}^{\frac{2}{3}}$+ex-1（x＜0）与g（x）=x${\;}^{\frac{2}{3}}$+ln（x+a）的图象上存在关于y轴对称的点，则a的取值范围是（　　）
    A．（-1，1）B．（-∞，$\frac{1}{\sqrt{e}}$）C．（-∞，1）D．（-∞，$\sqrt{e}$）

    查看答案和解析>>

    同步练习册答案