练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．（1-x）6（1+2x）展开式中含有x5项的系数为24．

    分析 （1-x）6（1+2x）的展开式中x5项由两部分相加得到：①（1+2x）中的常数项与（1-x）6展开式中的x5项； ②（1+2x）中的x项与（1-x）6展开式中的x4项．分别求系数再相加即可．

    解答 解：∵（1-x）6（1+2x）的展开式中x5项由两部分相加得到：
    ①（1+2x）中的常数项与（1-x）6展开式中的x5项
    ②（1+2x）中的x项与（1-x）6展开式中的x4项．
    分别求系数再相加即可．
    （1-x）6的展开式 的通项为Tr+1=（-1）rC6rxr，
    ∴（1-x）6（1+2x）的展开式中x5的系数等于-1×C65+2×C64=24，
    故答案为24．

    点评 本题考查二项式定理的应用，要注意本题中所求系数应由两部分组成．否则易出错．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．某公司生产的某产品每件成本为40元，经市场调查整理出如下信息：
    时间：（第x天）13610…
    日销量（m件）198194188180…
    ①该产品90天内日销量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
    ②该产品90天内销售价格（元/件）与时间（第x天）的关系如下表：
    时间：（第x天）1≤x＜5050≤x＜90
    销售价格（元/件）x+60100
    （1）求m关于x的函数关系；
    （2）设销售该产品每天利润为y元，求y关于x的函数表达式；并求出在90天内该产品哪天的销售利润最大？最大利润是多少？[每天利润=日销量x（销售价格-每件成本）]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．将y=sin（$ωx+\frac{π}{4}$）图象向右平移$\frac{π}{4}$单位长度后，与原图图象重合，则正数ω最小值为（　　）
    A．4B．8C．$\frac{1}{4}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知x，y满足约束条件$\left\{\begin{array}{l}x-y+5≥0\\ x+y≥0\\ x≤3.\end{array}\right.$，则z=3x-y的最小值为-10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．用秦九韶算法求f（x）=2x3-x2+4x+3，需要加法与乘法运算的次数分别为（　　）
    A．2，3B．3，3C．3，2D．2，2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知-$\frac{π}{2}$＜x＜0，sinx+cosx=$\frac{1}{5}$．
    （1）求sinx-cosx的值；   
     （2）求$\frac{1}{cos2x-sin2x}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

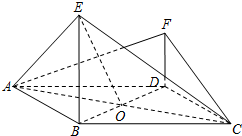    20．如图所示，四边形ABCD是边长为4菱形，O是AC与BD的交点，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF=2$\sqrt{2}$．
    （1）求证：EO⊥平面AFC；
    （2）求直线AE与直线CF所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知函数f（x）和g（x）均为奇函数，h（x）=a?f3（x）-b?g（x）-2在区间（0，+∞）上有最大值5，那么h（x）在（-∞，0）上的最小值为（　　）
    A．-5B．-9C．-7D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知$sin（\frac{π}{3}-α）=-\frac{2}{5}$，则$cos（\frac{2015π}{3}-2a）$=（　　）
    A．$\frac{7}{8}$B．$-\frac{7}{8}$C．$\frac{17}{25}$D．$-\frac{17}{25}$

    查看答案和解析>>

    同步练习册答案