
 在直三棱柱A1B1C1-ABC中,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,BC=CA=CC1,则BE与AF所成的角的余弦值是( )
在直三棱柱A1B1C1-ABC中,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,BC=CA=CC1,则BE与AF所成的角的余弦值是( )| A. | $\frac{\sqrt{30}}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{30}}{15}$ | D. | $\frac{\sqrt{15}}{10}$ |
分析 建立空间坐标系得出$\overrightarrow{BE}$=(-$\frac{a}{2}$,$\frac{a}{2}$,a),$\overrightarrow{AF}$=(0,-$\frac{a}{2}$,a),运用向量的数量积cosθ=|$\frac{\overrightarrow{AF}•BE}{|\overrightarrow{AF}|•|\overrightarrow{BE}|}$|=$\frac{\sqrt{30}}{10}$,求解夹角即可.
解答 解:建立空间坐标系得出如图: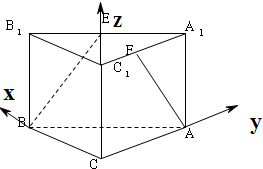
∵BC=CA=CC1=a,
∴根据题目条件得出:B(a,0,0),A(0,a,0),B1(a,0,a),A1(0,a,a),C1(0,0,a)
∵点E、F分别是A1B1、A1C1的中点,∴E($\frac{a}{2}$,$\frac{a}{2}$,a),F(0,$\frac{a}{2}$,a),
∴$\overrightarrow{BE}$=(-$\frac{a}{2}$,$\frac{a}{2}$,a),$\overrightarrow{AF}$=(0,-$\frac{a}{2}$,a)
∵$\overrightarrow{AF}$$•\overrightarrow{BE}$=$\frac{3{a}^{2}}{4}$,|$\overrightarrow{BE}$|=$\frac{\sqrt{6}}{2}$a,|$\overrightarrow{AF}$|=$\frac{\sqrt{5}}{2}$a,
∴cosθ=|$\frac{\overrightarrow{AF}•BE}{|\overrightarrow{AF}|•|\overrightarrow{BE}|}$|=$\frac{\sqrt{30}}{10}$,
故选:A
点评 本题考查了异面直线所成的夹角、三角形的中位线定理、余弦定理、勾股定理等基础知识与基本技能方法,属于基础题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 756种 | B. | 56种 | C. | 28种 | D. | 255种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{(1-ln2)\sqrt{10}}{5}$ | B. | $\frac{(1+ln2)\sqrt{10}}{5}$ | C. | $\frac{(3-ln2)\sqrt{10}}{5}$ | D. | $\frac{(3+ln2)\sqrt{10}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A、B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图1所示,B品牌的销售利润y2与投入资金x的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元).
某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A、B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图1所示,B品牌的销售利润y2与投入资金x的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(χ2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com