
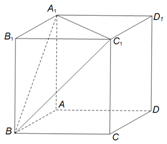
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )| A. | 2π | B. | $\frac{11π}{2}$ | C. | $\frac{16π}{3}$ | D. | $\frac{52π}{9}$ |
分析 由题意可知:B1D⊥平面A1BC1,|PD|+|PB1|=6>丨B1D丨=2$\sqrt{3}$,点P在一个“椭球”上运动,且被垂直于其对称轴的平面A1BC1截出一个圆,记其半径为r,根据勾股定理即可求得半径,求得圆的面积.
解答 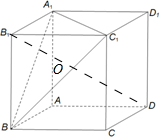 解:连接B1D,记B1D与平面A1BC1交于点O,易证B1D⊥平面A1BC1,丨OD丨=2丨OB1丨=$\frac{4\sqrt{3}}{3}$.由|PD|+|PB1|=6>丨B1D丨=2$\sqrt{3}$,
解:连接B1D,记B1D与平面A1BC1交于点O,易证B1D⊥平面A1BC1,丨OD丨=2丨OB1丨=$\frac{4\sqrt{3}}{3}$.由|PD|+|PB1|=6>丨B1D丨=2$\sqrt{3}$,
点P在一个“椭球”上运动,且被垂直于其对称轴的平面A1BC1截出一个圆,记其半径为r,记丨PD丨=a,
则$\left\{\begin{array}{l}{丨OD{丨}^{2}+{r}^{2}=丨PD{丨}^{2}={a}^{2}}\\{丨O{B}_{1}{丨}^{2}+{r}^{2}=丨P{B}_{1}{丨}^{2}=(6-a)^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{10}{3}}\\{{r}^{2}=\frac{52}{9}}\end{array}\right.$,
所以点P的轨迹所形成的图形的面积S=πr2=$\frac{52π}{9}$,
故选D.
点评 本题考查椭圆的定义,考查勾股定理的应用,考查计算能力,数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| X | -1 | 0 | 1 | 2 |
| P | a | b | c | $\frac{5}{18}$ |
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1),(0,+∞) | B. | (-∞,-1)∪(0,+∞) | C. | (-1,0) | D. | (-∞,0),(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ?p∧?q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com