
分析 (Ⅰ)由an>0,则做差an+1-an=$\frac{{a}_{n}}{{{a}_{n}}^{2}+1}$-an=$\frac{-{a}_{n}^{3}}{{a}_{n}^{2}+1}$<0,即可证明an+1<an;
(Ⅱ)由an+1>$\frac{1}{2}$an,an>$\frac{1}{2}$an-1≥($\frac{1}{2}$)2an-1≥…≥($\frac{1}{2}$)2an-1≥($\frac{1}{2}$)n-1a1=$\frac{1}{{2}^{n}}$,则an≥$\frac{1}{{2}^{n-1}}$.由$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=an,采用“累加法”即可求得$\frac{1}{{a}_{n}}$≥3-($\frac{1}{2}$)n-2=$\frac{3•{2}^{n-2}-1}{{2}^{n-2}}$=$\frac{3•{2}^{n}-4}{{2}^{n}}$,即可求得$\frac{1}{{2}^{n-1}}$≤an≤$\frac{{2}^{n}}{3•{2}^{n}-4}$.
解答 解:(Ⅰ)证明:由a1=1,an+1=$\frac{{a}_{n}}{{{a}_{n}}^{2}+1}$,得an>0,(n∈N),
则an+1-an=$\frac{{a}_{n}}{{{a}_{n}}^{2}+1}$-an=$\frac{-{a}_{n}^{3}}{{a}_{n}^{2}+1}$<0,
∴an+1<an;
(Ⅱ)证明:由(Ⅰ)知0<an<1,又an+1=$\frac{{a}_{n}}{{{a}_{n}}^{2}+1}$.,∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{1}{{a}_{n}^{2}+1}$≥$\frac{1}{2}$,即an+1>$\frac{1}{2}$an,
∴an>$\frac{1}{2}$an-1≥($\frac{1}{2}$)2an-1≥…≥($\frac{1}{2}$)2an-1≥($\frac{1}{2}$)n-1a1=$\frac{1}{{2}^{n}}$,即an≥$\frac{1}{{2}^{n-1}}$.
由an+1=$\frac{{a}_{n}}{{{a}_{n}}^{2}+1}$,则$\frac{1}{{a}_{n+1}}$=an+$\frac{1}{{a}_{n}}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=an,
∴$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$=a1=1,$\frac{1}{{a}_{3}}$-$\frac{1}{{a}_{2}}$=a2=$\frac{1}{2}$,$\frac{1}{{a}_{4}}$-$\frac{1}{{a}_{3}}$=a3=($\frac{1}{2}$)2…$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=an-1≥($\frac{1}{2}$)n-2,
累加得$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$=1+$\frac{1}{2}$+($\frac{1}{2}$)2+…+($\frac{1}{2}$)n-2=$\frac{1-\frac{1}{{2}^{n-1}}}{1-\frac{1}{2}}$=2-($\frac{1}{2}$)n-2,
而a1=1,
∴$\frac{1}{{a}_{n}}$≥3-($\frac{1}{2}$)n-2=$\frac{3•{2}^{n-2}-1}{{2}^{n-2}}$=$\frac{3•{2}^{n}-4}{{2}^{n}}$,
∴an≤$\frac{{2}^{n}}{3•{2}^{n}-4}$.
综上得$\frac{1}{{2}^{n-1}}$≤an≤$\frac{{2}^{n}}{3•{2}^{n}-4}$.
点评 本题考查数列的通项公式,考查数列与不等式的综合应用,考查“放缩法”的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2粒 | B. | 4粒 | C. | 3粒 | D. | 5粒 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.81 | B. | 0.9 | C. | 0.64 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0,4a+b=0 | B. | a<0,4a+b=0 | C. | a>0,2a+b=0 | D. | a<0,2a+b=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
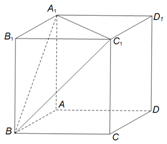 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )| A. | 2π | B. | $\frac{11π}{2}$ | C. | $\frac{16π}{3}$ | D. | $\frac{52π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com