
函数g(x)=ax3+2(1-a)x2-3ax在区间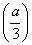 内单调递减,则a的取值范围是________.
内单调递减,则a的取值范围是________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
若点P在曲线y=x3-3x2+(3-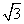 )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
A.[0,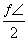 ) B.[0,
) B.[0,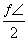 )∪[
)∪[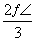 ,π) C.[
,π) C.[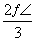 ,π) D.[0,
,π) D.[0,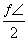 )∪(
)∪(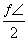 ,
,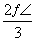 ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个结论:①由曲线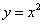 、
、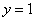 围成的区域的面积为
围成的区域的面积为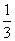 ; ② “
; ② “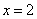 ”是“向量
”是“向量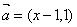 与向量
与向量 平行”的充分非必要条件; ③命题“
平行”的充分非必要条件; ③命题“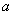 、
、 都是有理数”的否定是“
都是有理数”的否定是“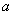 、
、 都不是有理数”;④函数
都不是有理数”;④函数 的最小值等于
的最小值等于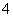 。其中正确结论的个数为
。其中正确结论的个数为
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com