
分析 求出${f}^{'}(x)=\frac{1}{x}+e-a$,x>0,当a≤e时,f′(x)>0,f(x)≤0不可能恒成立,当a>e时,由${f}^{'}(x)=\frac{1}{x}+e-a=0$,得x=$\frac{1}{a-e}$,由题意当x=$\frac{1}{a-e}$时,f(x)取最大值0,推导出$\frac{b}{a}≥\frac{-1-ln(a-e)}{a}$(a>e),令F(x)=$\frac{-1-ln(x-e)}{x}$,x>e,F′(x)=$\frac{(x-e)ln(x-e)-e}{(x-e){x}^{2}}$,令H(x)=(x-e)ln(x-e)-e,H′(x)=ln(x-e)+1,由此利用导数性质能求出$\frac{b}{a}$的最小值.
解答 解:∵函数f(x)=lnx+(e-a)x-b,其中e为自然对数的底数,
∴${f}^{'}(x)=\frac{1}{x}+e-a$,x>0,
当a≤e时,f′(x)>0,
f(x)在(0,+∞)上是增函数,∴f(x)≤0不可能恒成立,
当a>e时,由${f}^{'}(x)=\frac{1}{x}+e-a=0$,得x=$\frac{1}{a-e}$,
∵不等式f(x)≤0恒成立,∴f(x)的最大值为0,
当x∈(0,$\frac{1}{a-e}$)时,f′(x)>0,f(x)单调递增,
当x∈($\frac{1}{a-e}$,+∞)时,f′(x)<0,f(x)单调递减,
∴当x=$\frac{1}{a-e}$时,f(x)取最大值,
f($\frac{1}{a-e}$)=-ln(a-e)-b-1≤0,
∴ln(a-e)+b+1≥0,
∴b≥-1-ln(a-e),
∴$\frac{b}{a}≥\frac{-1-ln(a-e)}{a}$(a>e),
令F(x)=$\frac{-1-ln(x-e)}{x}$,x>e,
F′(x)=$\frac{-\frac{1}{x-e}x+1+ln(x-e)}{{x}^{2}}$=$\frac{(x-e)ln(x-e)-e}{(x-e){x}^{2}}$,
令H(x)=(x-e)ln(x-e)-e,
H′(x)=ln(x-e)+1,
由H′(x)=0,得x=e+$\frac{1}{e}$,
当x∈(e+$\frac{1}{e}$,+∞)时,H′(x)>0,H(x)是增函数,
x∈(e,e+$\frac{1}{e}$)时,H′(x)<0,H(x)是减函数,
∴当x=e+$\frac{1}{e}$时,H(x)取最小值H(e+$\frac{1}{e}$)=-e-$\frac{1}{e}$,
∵x→e时,H(x)→0,x>2e时,H(x)>0,H(2e)=0,
∴当x∈(e,2e)时,F′(x)<0,F(x)是减函数,
当x∈(2e,+∞)时,F′(x)>0,F(x)是增函九,
∴x=2e时,F(x)取最小值,F(2e)=$\frac{-1-1}{2e}$=-$\frac{1}{e}$,
∴$\frac{b}{a}$的最小值为-$\frac{1}{e}$.
故答案为:-$\frac{1}{e}$.
点评 本题考查两数比值的最小值的求法,是中档题,解题时要认真审题,注意导数性质和构造法的合理运用.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则a+c≤b+c | B. | 若a+c≤b+c,则a≤b | C. | 若a+c>b+c,则a>b | D. | 若a≤b,则a+c≤b+c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{8}-\frac{y^2}{24}=1$ | B. | $\frac{x^2}{24}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
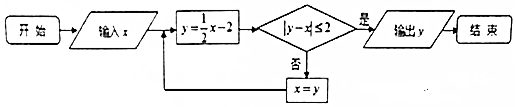
| A. | 2 | B. | -1 | C. | -$\frac{13}{4}$ | D. | -$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6}}]$ | B. | $[{-\frac{1}{6},\frac{1}{6}}]$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $[{-\frac{1}{3},\frac{1}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
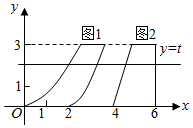 我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.
我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com