
| A. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$ |
分析 如图所示,$\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{EC}$,$\overrightarrow{EC}$=$\frac{1}{2}\overrightarrow{AC}$,$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{DC}$,$\overrightarrow{DC}=\frac{1}{2}\overrightarrow{BC}$,即可得出.
解答 解:如图所示,
$\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{EC}$,$\overrightarrow{EC}$=$\frac{1}{2}\overrightarrow{AC}$,$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{DC}$,$\overrightarrow{DC}=\frac{1}{2}\overrightarrow{BC}$,
∴$\overrightarrow{BC}$=$\overrightarrow{BE}$+$\frac{1}{2}(\overrightarrow{AD}+\frac{1}{2}\overrightarrow{BC})$,
化为$\overrightarrow{BC}$=$\frac{2}{3}\overrightarrow{a}$+$\frac{4}{3}\overrightarrow{b}$.
故选:A.
点评 本题考查了向量的三角形法则、向量共线定理、平面向量基本定理,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8\sqrt{15}}{5}$ | B. | $\sqrt{15}$ | C. | $\frac{\sqrt{15}}{2}$ | D. | 6$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
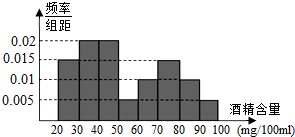 据《南通日报》报道,2015年1月1日至1月31日,市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.(酒精含量≥80mg/100ml为醉酒驾车)
据《南通日报》报道,2015年1月1日至1月31日,市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.(酒精含量≥80mg/100ml为醉酒驾车)| 酒精含量(单位:mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) |
| 人数 | 16 | 16 | 4 | |
| 酒精含量(单位:mg/100ml) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com