
 Ϊ������ѧ������ѧ��ģ��Ӧ��������ijУ��֯��һ��ʵ�ز��������ͼ���������������ľAE�ĸ߶�H��m������ֱ���õı��BC�ĸ߶�h=4m�����ǡ�ABE=������ADE=�£�D��C��E���㹲�ߣ����Ը������������������ش��������⣺
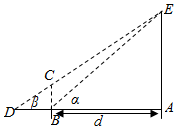
Ϊ������ѧ������ѧ��ģ��Ӧ��������ijУ��֯��һ��ʵ�ز��������ͼ���������������ľAE�ĸ߶�H��m������ֱ���õı��BC�ĸ߶�h=4m�����ǡ�ABE=������ADE=�£�D��C��E���㹲�ߣ����Ը������������������ش��������⣺���� ��1����Rt��ABE�пɵ�AD=$\frac{H}{tan��}$����Rt��ADE�пɵ�AB=$\frac{H}{tan��}$��BD=$\frac{h}{tan��}$���ٸ���AD-AB=DB���ɵõ�H��
��2������d�ֱ��ʾ��tan����tan�£��ٸ������Ǻ�ʽ�����tan����-�£��������ɻ�������ʽ����ʽ���ٸ��ݻ�������ʽ�����tan����-�£������ֵ����-�������ֵ���õ��𰸣�
��� �⣺��1����Rt��ABE�пɵ�AD=$\frac{H}{tan��}$��
��Rt��ADE�пɵ�AB=$\frac{H}{tan��}$��BD=$\frac{h}{tan��}$��
��AD-AB=DB���ʵ�$\frac{H}{tan��}-\frac{H}{tan��}=\frac{h}{tan��}$��
�ã�H=$\frac{htan��}{tan��-tan��}$=$\frac{4��\sqrt{3}}{\sqrt{3}-\frac{\sqrt{3}}{3}}$=6��
��ˣ��������ľ�ĸ߶�H��6m��
��2��������֪d=AB����tan��=$\frac{H}{d}$��tan��=$\frac{H}{AD}$=$\frac{h}{BD}$=$\frac{H-h}{d}$��
tan����-�£�=$\frac{tan��-tan��}{1+tan��tan��}$=$\frac{\frac{H}{d}-\frac{H-h}{d}}{1+\frac{H}{d}•\frac{H-h}{d}}$=$\frac{hd}{{d}^{2}+H��H-h��}$=$\frac{h}{d+\frac{H��H-h��}{d}}$
$��\frac{h}{2\sqrt{d•\frac{H��H-h��}{d}}}$=$\frac{h}{2\sqrt{H��H-h��}}$�������ҽ���d=$\sqrt{H��H-h��}$��ʱ��ȡ�Ⱥţ�
�ʵ�H=8ʱ��d=4$\sqrt{2}$��tan����-�£����
��Ϊ0���£�����$\frac{��}{2}$����0����-�£�$\frac{��}{2}$�����Ե�d=4$\sqrt{2}$ʱ����-�����
���� ������Ҫ����������ε�֪ʶ�����Dz�����м�����ʽ��Ӧ�ã����漰��ֵ����ʱ���ɿ����ò���ʽ�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2��3��4��5 | B�� | 2��4��6��8��10 | C�� | 4��14��24��34��44 | D�� | 5��16��27��38��49 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �Ŷ����� | 0 | 1 | 2 | 3 | 4 | 4�� ���� |
| Ƶ�� | 0.1 | 0.15 | 0.15 | x | 0.25 | 0.15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow a$-$\frac{1}{2}$$\overrightarrow b$ | B�� | $\overrightarrow a$+$\frac{1}{2}$$\overrightarrow b$ | C�� | $\frac{1}{2}$$\overrightarrow b$-$\overrightarrow a$ | D�� | $\frac{1}{2}$$\overrightarrow b$+$\overrightarrow a$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0.8 | C�� | 0.6 | D�� | 0.3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com