练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．在某超市收银台排队付款的人数及其频率如表：
     排队人数 0 1 2 34  4人 以上
     频率0.1  0.15 0.15x 0.25 0.15 
    视频率为概率，则至少有2人排队付款的概率为0.75．（用数字作答）

    分析 利用对立事件概率计算公式直接求解．

    解答 解：视频率为概率，
    由某超市收银台排队付款的人数及其频率表得到至少有2人排队付款的概率为：
    p=1-0.1-0.15=0.75．
    故答案为：0.75．

    点评 本题考查概率的求法，考查对立事件概率计算公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．已知函数f（x）=ax3+（a+2）x2-1（x∈R）为偶函数，则曲线y=f（x）在点（2，f（2））处的切线的方程为8x-y-9=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某企业生产的一种产品的广告费用x（单位：万元）与销售额y（单位：万元）的统计数据如表：
     广告费用x 1 2 3 4 5
     销售额y 10 15 25 45 55
    （1）根据上述数据，求出销售额y（万元）关于广告费用x（万元）的线性回归方程；
    （2）如果企业要求该产品的销售额不少于36万元，则投入的广告费用应不少于多少万元？
    （参考数值：$\sum_{i=1}^{5}{x}_{i}=15$，$\sum_{i=1}^{5}{y}_{i}=150$，$\sum_{i=1}^{5}{x}_{i}{y}_{i}=570$，$\sum_{i=1}^{5}{{x}_{i}}^{2}=55$，$\sum_{i=1}^{5}{{y}_{i}}^{2}=6000$．

    回归直线的斜率和截距的最小二乘估计公式分别为：$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$，$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知函数f（x）=x2+ex-$\frac{1}{2}$（x＞0）与g（x）=x2+ln（x+a）的图象上存在关于y轴对称的点，则a的取值范围是（　　）
    A．（-$\sqrt{e}$，$\sqrt{e}$）B．（-$\sqrt{e}$，+∞）C．（-∞，$\sqrt{e}$）D．（$\sqrt{e}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．（2x+$\frac{a}{x}$）（x-$\frac{2}{x}$）5的展开式中各项系数的和为-1，则该展开式中常数项为（　　）
    A．-200B．-120C．120D．200

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知函数f（x）=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x，若其图象是由y=sin2x的图象向左平移φ（φ＞0）个单位得到的，则φ的最小值为（　　）
    A．$\frac{π}{12}$B．$\frac{π}{6}$C．$\frac{π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

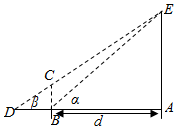    13．为了培养学生的数学建模和应用能力，某校组织了一次实地测量活动，如图，假设待测量的树木AE的高度H（m），垂直放置的标杆BC的高度h=4m，仰角∠ABE=α，∠ADE=β（D，C，E三点共线），试根据上述测量方案，回答如下问题：
    （1）若测得α=60°、β=30°，试求H的值；
    （2）经过分析若干次测得的数据后，大家一致认为适当调整标杆到树木的距离d（单位：m），使α与β之差较大时，可以提高测量精确度．
    若树木的实际高度为8m，试问d为多少时，α-β最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=4sinxcos（x-$\frac{π}{6}$）-1
    （1）求函数f（x）的最小正周期及其图象的对称中心坐标
    （2）求函数f（x）的单调增区间及f（x）在[0，$\frac{π}{2}$]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．在区间[0，4]内随机选一个实数x，该实数恰好在区间[1，3]内的概率是（　　）
    A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{3}{4}$

    查看答案和解析>>

    同步练习册答案