Question

20．如图（1），等腰梯形OABC的上、下底边长分别为1、3，底角为∠COA=60°．记该梯形内部位于直线x=t（t＞0）左侧部分的面积为f（t）．试求f（t）的解析式，并在如图（2）给出的坐标系中画出函数y=f（t）的图象．

Answer 1

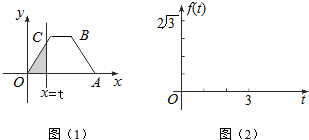
分析 过C、B分别作OA的垂线，垂足分别为D、E，设直线x=t与x轴的交点为P，
讨论P∈OD、DE、EA以及Ax时，求出函数f（t）的解析式，利用分段函数写出f（t）的解析式并画出函数的图象．

解答 解：如图所示，过C、B分别作OA的垂线，垂足分别为D、E，
设直线x=t与x轴的交点为P，
则|OD|=|DE|=|EA|=1，|CD|=|BE|=$\sqrt{3}$；
所以，①当P∈OD，即t∈（0，1]时，
f（t）=$\frac{1}{2}$•t•$\sqrt{3}$t=$\frac{\sqrt{3}}{2}$t²；
②当P∈DE，即t∈（1，2]时，
f（t）=$\frac{1}{2}$•[（t-1）+t]•$\sqrt{3}$=$\frac{\sqrt{3}}{2}$（2t-1）；
③当P∈EA，即t∈（2，3]时，
f（t）=$\frac{1}{2}$•（1+3）•$\sqrt{3}$-$\frac{\sqrt{3}}{2}$•（3-t）²=$\frac{\sqrt{3}}{2}$（-t²+6t-5）；
④当P∈Ax，即t∈（3，+∞）时，
f（t）=$\frac{1}{2}$•（1+3）•$\sqrt{3}$=2$\sqrt{3}$；
综上，f（t）=$\left\{\begin{array}{l}{{\frac{\sqrt{3}}{2}t}^{2}，t∈（0，1]}\\{\frac{\sqrt{3}}{2}（2t-1），t∈（1，2]}\\{\frac{\sqrt{3}}{2}（{-t}^{2}+6t-5），t∈（2，3]}\\{2\sqrt{3}，t∈（3，+∞）}\end{array}\right.$；
画出函数f（t）的图象如图2所示．

点评 本题考查了求分段函数的解析式、画分段函数的图象的应用问题，是基础题目．