
���� ��1���ɹ���Q����b=$\sqrt{3}$����ã���PF1F2������ΪG�����꣬��IG��F1F2��|y0|=3r�����������ε������ʽ��֪a=2c���������a��b��ֵ�������Բ���̣�
��2��������Բ�����߷�Ũ�������ֱ��AB�ķ��̣��ɵ�MΪֱ��x-y=4�ϣ���������������ö������꣮
��� �⣺��1������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������x���ϣ��ҹ���$Q��0��\sqrt{3}��$��
��$b=\sqrt{3}$����1�֣�
���PF1F2����Բ�İ뾶Ϊr����P������Ϊ��x0��y0����
���PF1F2����G������Ϊ$��\frac{x_0}{3}��\frac{y_0}{3}��$��
��IG��F1F2��
��|y0|=3r������2�֣�
�ɡ�PF1F2����ɵ�$\frac{1}{2}��|P{F_1}|+|P{F_2}|+|{F_1}{F_2}|$��r=$\frac{1}{2}|{F_1}{F_2}||{y_0}|$��
��a=2c��$��c=\sqrt{{a^2}-{b^2}}��$������4�֣�
����$a=2��b=\sqrt{3}$��
���������Բ����Ϊ����Բ����Ϊ$\frac{x^2}{4}+\frac{y^2}{3}=1$����5�֣�
��2����M��x1��y1����A��x2��y2����B��x3��y3��������MA��MB�ķ��̷ֱ�Ϊ$\frac{{{x_2}x}}{4}+\frac{{{y_2}y}}{3}=1$��$\frac{{{x_3}x}}{4}+\frac{{{y_3}y}}{3}=1$������7�֣�
�ߵ�M�����������ϣ�
��$\frac{{{x_2}{x_1}}}{4}+\frac{{{y_2}{y_1}}}{3}=1$��$\frac{{{x_3}{x_1}}}{4}+\frac{{{y_3}{y_1}}}{3}=1$��
��ֱ��AB�ķ���Ϊ$\frac{{{x_1}x}}{4}+\frac{{{y_1}y}}{3}=1$������9�֣�
�֡ߵ�MΪֱ��x-y=4�ϣ�
��y1=x1-4
��ֱ��AB�ķ��̿ɻ�Ϊ$\frac{{{x_1}x}}{4}+\frac{{��{x_1}-4��y}}{3}=1$�������ã�3x+4y��x1=16y+12��
��$\left\{\begin{array}{l}3x+4y=0\\ 16y+12=0\end{array}\right.$���$\left\{\begin{array}{l}x=1\\ y=-\frac{3}{4}\end{array}\right.$��
��ˣ�ֱ��AB������$��1��-\frac{3}{4}��$������12�֣�
���� ���⿼����Բ�ı����̼��������ʣ����������ε����Ĺ�ʽ�������ε������ʽ����Բ�����߹�ʽ��������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 8�� | C�� | 12�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16�� | B�� | 64�� | C�� | $\frac{32}{3}$�� | D�� | 32�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
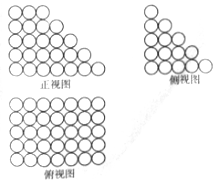 ������ѧ����������Ҫ��ѧ�ɾ�֮һΪ϶��������ν϶����������֮��϶���ߣ������塢��̳֮�࣬���ֳ���̨��״������������϶����n�㣬�ϵ���a��b��������ɣ����¸���ij��������θ�����һ�����壬���²㣨���µף���c��d��������ɣ�����������϶�������������Ĺ�ʽΪS=$\frac{n}{6}$[��2b+d��a+��b+2d��c]+$\frac{n}{6}$��c-a������֪�����ɸ���ͬС��ճ���ɵļ�������������ͼ��ͼ��ʾ����ö��������С��ĸ���Ϊ��������
������ѧ����������Ҫ��ѧ�ɾ�֮һΪ϶��������ν϶����������֮��϶���ߣ������塢��̳֮�࣬���ֳ���̨��״������������϶����n�㣬�ϵ���a��b��������ɣ����¸���ij��������θ�����һ�����壬���²㣨���µף���c��d��������ɣ�����������϶�������������Ĺ�ʽΪS=$\frac{n}{6}$[��2b+d��a+��b+2d��c]+$\frac{n}{6}$��c-a������֪�����ɸ���ͬС��ճ���ɵļ�������������ͼ��ͼ��ʾ����ö��������С��ĸ���Ϊ��������| A�� | 83 | B�� | 84 | C�� | 85 | D�� | 86 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��[1��2]��x2-3x+2��0 | B�� | ?x∉[1��2]��x2-3x+2��0 | ||
| C�� | $?{x_0}��[{1��2}]��{x_0}^2-3{x_0}+2��0$ | D�� | $?{x_0}∉[{1��2}]��{x_0}^2-3{x_0}+2��0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
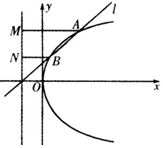 ��ͼ����ֱ֪��l��y=k��x+1����k��0����������C��y2=4x�ཻ��A��B���㣬��FΪ�����߽��㣬��A��B������������C���ϵ���Ӱ�ֱ���M��N����|AM|=2|BN|����k��ֵ��$\frac{2}{3}\sqrt{2}$��
��ͼ����ֱ֪��l��y=k��x+1����k��0����������C��y2=4x�ཻ��A��B���㣬��FΪ�����߽��㣬��A��B������������C���ϵ���Ӱ�ֱ���M��N����|AM|=2|BN|����k��ֵ��$\frac{2}{3}\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com