
【题目】如图,已知长方体ABCD-A1B1C1D1中,AB=3,BC=2,CC1=5,E是棱CC1上不同于端点的点,且![]() .
.
(1) 当∠BEA1为钝角时,求实数λ的取值范围;
(2) 若λ=![]() ,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
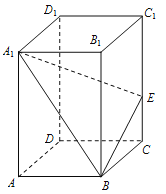
【答案】(1)(![]() ,
,![]() ).(2)
).(2)![]() .
.
【解析】
试题解析:
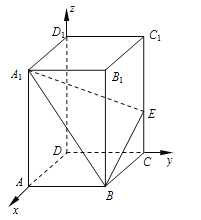
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立如图所示的空间直角坐标系.
由题设,知B(2,3,0),A1(2,0,5),C(0,3,0),C1(0,3,5).
因为![]() ,所以E(0,3,5λ).
,所以E(0,3,5λ).
从而![]() =(2,0,-5λ),
=(2,0,-5λ),![]() =(2,-3,5-5λ). 2分
=(2,-3,5-5λ). 2分
当∠BEA1为钝角时,cos∠BEA1<0,
所以![]() <0,即2×2-5λ(5-5λ)<0,
<0,即2×2-5λ(5-5λ)<0,
解得![]() <λ<
<λ<![]() .
.
即实数λ的取值范围是(![]() ,
,![]() ). 5分
). 5分
(2)当λ=![]() 时,
时,![]() =(2,0,-2),
=(2,0,-2),![]() =(2,-3,3).
=(2,-3,3).
设平面BEA1的一个法向量为n1=(x,y,z),
由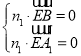 得
得![]()
取x=1,得y=![]() ,z=1,
,z=1,
所以平面BEA1的一个法向量为n1=(1,![]() ,1). 7分
,1). 7分
易知,平面BA1B1的一个法向量为n2=(1,0,0).
因为cos< n1,n2>=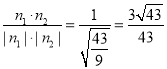 ,
,
从而|cosθ|=![]() . 10分
. 10分


科目:高中数学 来源: 题型:
【题目】已知集合A={x|﹣2≤x≤5},B={x|m+1≤x≤2m﹣1}.
(1)当m=3时,求集合A∩B,A∪B;
(2)若BA,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中实数
其中实数![]() 为常数且
为常数且![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若函数![]() 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数![]() 的取值范围及所有极值之和;
的取值范围及所有极值之和;
(III)在(II)的条件下,记![]() 分别为函数
分别为函数![]() 的极大值点和极小值点,
的极大值点和极小值点,
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() 的长轴是短轴的两倍,点
的长轴是短轴的两倍,点![]() 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 恰好构成等比数列,记△
恰好构成等比数列,记△![]() 的面积为S.
的面积为S.
(1)求椭圆C的方程.
(2)试判断![]() 是否为定值?若是,求出这个值;若不是,请说明理由?
是否为定值?若是,求出这个值;若不是,请说明理由?
(3)求S的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租地建仓库,每月土地占用费y1与车库到车站的距离x成反比,而每月的库存货物的运费y2与车库到车站的距离x成正比.如果在距离车站10公里处建立仓库,这两项费用y1和y2分别为2万元和8万元.求若要使得这两项费用之和最小时,仓库应建在距离车站多远处?此时最少费用为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 . 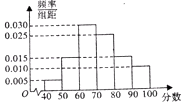
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环保节能设备生产企业的产品供不应求,已知某种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=150﹣ ![]() x,每套的售价不低于90万元;月产量x(套)与生产总成本y2(万元)之间满足关系式y2=600+72x,则月生产多少套时,每套设备的平均利润最大?最大平均利润是多少?
x,每套的售价不低于90万元;月产量x(套)与生产总成本y2(万元)之间满足关系式y2=600+72x,则月生产多少套时,每套设备的平均利润最大?最大平均利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com