
分析 (Ⅰ)n=1,n=2代值计算即可;
(Ⅱ)推出Sn-12的表达式,与Sn2相减可得an2=2Sn-an,得an-12的表达式,从而可得数列an是首项为1,公差为1的等差数列;
(Ⅲ)an•ln(1+$\frac{1}{{a}_{n}}$)=nln(1+$\frac{1}{n}$),由n=1时,nln(1+$\frac{1}{n}$)=ln2,要证ln2<an•ln(1+$\frac{1}{{a}_{n}}$)<ln3.(n>1),即证ln2<ln(1+$\frac{1}{n}$)n<ln3,即为2<(1+$\frac{1}{n}$)n<3成立.运用二项式定理和放缩法,结合不等式的性质,即可得证.
解答 解:(Ⅰ)∵对任意的n∈N*,都有an>0,Sn=$\sqrt{{a_1}^3+{a_2}^3+…+{a_n}^3}$,
∴a13+a23+…+an3=Sn2,
∴当n=1时,a12=S12=a13,
又∵an>0,∴a1=1,
∵(a1+a2)2=a13+a23,
又∵a2>0,
∴a2=2;
(Ⅱ)∵a13+a23++an3=Sn2①
∴当n≥2时,a13+a23++an-13=Sn-12②
由①-②得,an3=Sn2-Sn-12=(Sn-Sn-1)(Sn+Sn-1)=an(Sn+Sn-1)
∴an2=Sn+Sn-1=2Sn-an(n≥2)
显然当n=1时,a1=1适合上式.
故an2=2Sn-an(n∈N*)③
an-12=2Sn-1-an-1(n≥2)④
由③-④得,an2-an-12=2Sn-2Sn-1-an+an-1=an+an-1
∵an+an-1>0,∴an-an-1=1(n≥2)
故数列an是首项为1,公差为1的等差数列.
∴an=n(n∈N*),
(Ⅲ)证明:∵an•ln(1+$\frac{1}{{a}_{n}}$)=nln(1+$\frac{1}{n}$),
由n=1时,nln(1+$\frac{1}{n}$)=ln2,
要证ln2<an•ln(1+$\frac{1}{{a}_{n}}$)<ln3.(n>1),
即证ln2<ln(1+$\frac{1}{n}$)n<ln3,
即为2<(1+$\frac{1}{n}$)n<3成立.
由(1+$\frac{1}{n}$)n=Cn0+Cn1$\frac{1}{n}$+Cn2($\frac{1}{n}$)2+…+Cnn($\frac{1}{n}$)n
=1+1+Cn2×$\frac{1}{{n}^{2}}$+Cn3×$\frac{1}{{n}^{3}}$+…+Cnn×$\frac{1}{{n}^{n}}$
=2+$\frac{1}{2!}$×$\frac{n(n-1)}{{n}^{2}}$+$\frac{1}{3!}$×$\frac{n(n-1)(n-2)}{{n}^{3}}$+…+$\frac{1}{n!}$×$\frac{n•(n-1)…2•1}{{n}^{n}}$
<2+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{n!}$<2+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}}$
=2+$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n-1}]}{1-\frac{1}{2}}$=3-($\frac{1}{2}$)n-1<3.
显然(1+$\frac{1}{n}$)n=1+1+Cn2×$\frac{1}{{n}^{2}}$+Cn3×$\frac{1}{{n}^{3}}$+…+Cnn×$\frac{1}{{n}^{n}}$>2.
所以2<(1+$\frac{1}{n}$)n<3.
则ln2≤an•ln(1+$\frac{1}{{a}_{n}}$)<ln3.
点评 此题主要考查等比数列的性质及递推公式的应用,考查转化思想和二项式定理的运用及放缩法,难度比较大,此题综合性较强,做题时要认真学会独立思考.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{7}{12}$,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{4}$,$\frac{7}{12}$) | D. | ($\frac{1}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
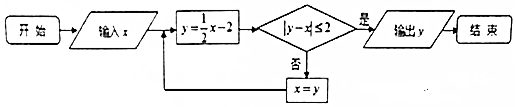
| A. | 2 | B. | -1 | C. | -$\frac{13}{4}$ | D. | -$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
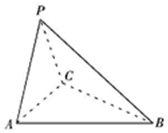 如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.
如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com