练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知集合A={x|x=|a|，a∈R且a≠0}，B={y|y=|b-1998|，b∈R}，求证：A?B．
    考点：集合的包含关系判断及应用
    专题：集合
    分析：利用绝对值的意义和集合之间的关系即可证明．
    解答： 证明：对于集合A：∵a∈R且a≠0，∴x=|a|＞0，∴A=（0，+∞）．
    B对于集合A：∵b∈R，∴y=|b-1998|≥0，∴B=[0，+∞）．
    ∴A?B．
    点评：本题考查了绝对值的意义和集合之间的关系，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    曲线C上的动点P是坐标为（
    		3
    cosθ，
    		2
    sinθ）．
    （1）求曲线C的普通方程，并指出曲线的类型及焦点坐标；
    （2）过点Q（2，1）作曲线C的两条切线l1、l2，证明l1⊥l2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，四面体ABCD中，平面ABC⊥平面BCD，AC=AB，CB=CD，∠DCB=120°．点E在BD上，且DE=
    1
    3
    DB．
    （Ⅰ）求证：AB⊥CE；
    （Ⅱ）若AC=CE，求二面角A-CD-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

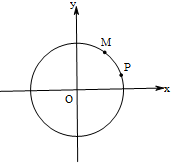    已知圆O：x2+y2=4．
    （1）直线l1：
    		3
    x+y-2
    		3
    =0与圆O相交于A、B两点，求|AB|；
    （2）如图，设M（x1，y1）、P（x2，y2）是圆O上的两个动点，点M关于原点的对称点为M1，点M关于x轴的对称点为M2，如果直线PM1、PM2与y轴分别交于（0，m）和（0，n），问m•n是否为定值？若是求出该定值；若不是，请说明理由；
    （3）过O点任作一直线与直线x=4交于E点，过（2，0）点作直线与OE垂直，并且交直线x=4于F点，以EF为直径的圆是否过定点，如过定点求出其坐标，如不过，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定点F（0，1）和直线l1：y=-1，过定点F与直线l1相切的动圆圆心为点C．
    （1）求动点C的轨迹方程；
    （2）过点F的直线l2交动点C的轨迹于两点P、Q，交直线l1于点R，求
    RP
    •
    RQ
    的最小值；
    （3）过点F且与l2垂直的直线l3交动点C的轨迹于两点R、T，问四边形PRQT的面积是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

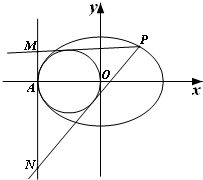    如图，离心率为
    		2
    2
    的椭圆
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）与直线l：x=-2相切于点A（-2，0）．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）若OA是圆C的直径，P（x0，y0）（x0＞0）为椭圆上的动点，过P作圆C的两条切线，分别交直线l于点M、N，求当
    PM
    •
    PN
    取得最小值时P点的横坐标x0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若抛物线y2=2px的一个焦点与椭圆
    x2
    6
    +
    y2
    2
    =1的右焦点重合，
    （1）求P的值；
    （2）若点P（2，4）是抛物线上一点，点F为抛物线的焦点，求线段PF的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

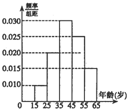    某市交管部门为了宣传新交规举办交通知识问答活动，随机对该市15～65岁的人群抽样了n人，回答问题统计结果如图表所示：
     分组回答正确的人数回答正确的人数
    占本组的频率
    第1组[15，25）50.5
    第2组[25，35） a0.9
    第3组[35，45）27 x
    第4组[45，55） b0.36
    第5组[55，65）3 y
    （1）分别求出a，b，x，y的值；
    （2）从第2，3，4组回答正确的人中用分层抽样方法抽取6人，则第2，3，4组每组应各抽取多少人？
    （3）在（2）的前提下，决定在所抽取的6人中随机抽取2人颁发幸运奖，求：所抽取的2人中至少有一个第2组的人的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知F1、F2是椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的两个焦点，P为椭圆C上一点，且
    PF1
    ⊥
    PF2
    ．若△PF1F2的面积为16，则b=
     
    ．

    查看答案和解析>>

    同步练习册答案