
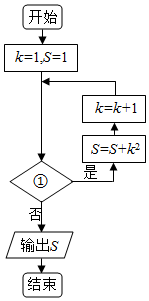
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加变量k的平方到S并输出S,模拟程序的执行过程,分析出进行循环的条件,可得答案.
解答 解:模拟执行程序,可得
k=1,S=1
满足条件,执行循环体,S=2,k=2
满足条件,执行循环体,S=6,k=3
满足条件,执行循环体,S=15,k=4
由题意,此时应该不满足条件,退出循环,输出S的值为15,
所以判断框内可填写“k<4”,
故答案为:k<4.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误,本题属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$).
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
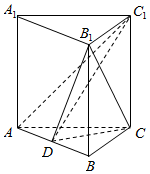 如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.
如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
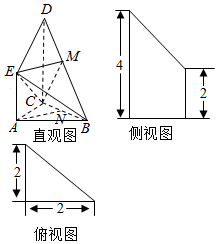 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com