
分析 (Ⅰ)由三角函数中的恒等变换应用化简解析式可得f(x)=$-sin({2ax+\frac{π}{6}})$,根据题意b为f(x)的最大值或最小值,可求b,由已知求周期后,根据周期公式即可求得a.
(Ⅱ)由题意知$sin({4{x_0}+\frac{π}{6}})=0$,则可求${x_0}=\frac{kπ}{4}-\frac{π}{24}({k∈Z})$,由$0≤\frac{kπ}{4}-\frac{π}{24}≤\frac{π}{2}({k∈Z})$得k的值,从而可分类讨论得解.
解答 (本题满分为12分)
解:(Ⅰ)$f(x)={sin^2}ax-\sqrt{3}sinax•cosax-\frac{1}{2}=\frac{1-cos2ax}{2}-\frac{{\sqrt{3}}}{2}sin2ax-\frac{1}{2}$=$-sin({2ax+\frac{π}{6}})$
∵y=f(x)的图象与直线y=b相切,
∴b为f(x)的最大值或最小值,即b=-1或b=1,
∵切点横坐标依次成公差为$\frac{π}{2}$的等差数列,
∴f(x)的最小正周期为$\frac{π}{2}$,即$T=\frac{2π}{{|{2a}|}}=\frac{π}{2}$,a>0,
∴a=2,即$f(x)=-sin({4x+\frac{π}{6}})$;…(6分)
(Ⅱ)由题意知$sin({4{x_0}+\frac{π}{6}})=0$,则$4{x_0}+\frac{π}{6}=kπ({k∈Z})$,
∴${x_0}=\frac{kπ}{4}-\frac{π}{24}({k∈Z})$,由$0≤\frac{kπ}{4}-\frac{π}{24}≤\frac{π}{2}({k∈Z})$得k=1或k=2,
因此${x_0}=\frac{5π}{24}$或${x_0}=\frac{11π}{24}$.
当${x_0}=\frac{5π}{24}$时,y=f(x)的单调增区间为$[{\frac{5π}{24},\frac{π}{3}}]$和$[{\frac{7π}{12},\frac{17π}{24}}]$,
当${x_0}=\frac{11π}{24}$时,y=f(x)的单调增区间为$[{\frac{7π}{12},\frac{5π}{6}}]$.…(12分)
点评 本题主要考查了三角函数中的恒等变换应用,等差数列的通项公式,三角函数的图象与性质,属于基本知识的考查.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:选择题
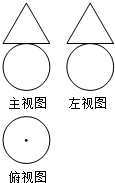 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )| A. | $\frac{4+\sqrt{3}}{3}$π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
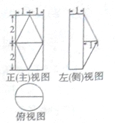
| A. | $\frac{16}{3}$ | B. | 5+$\frac{π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com