
| A. | ρ=2$\sqrt{2}$cos θ | B. | ρ=-2$\sqrt{2}$cos θ | C. | ρ=2$\sqrt{2}$sin θ | D. | ρ=-2$\sqrt{2}$sin θ |
分析 ($\sqrt{2}$,π)化为直角坐标$(-\sqrt{2},0)$,可得圆的直角坐标方程:$(x+\sqrt{2})^{2}$+y2=2,展开利用互化公式即可得出.
解答 解:($\sqrt{2}$,π)化为直角坐标$(-\sqrt{2},0)$,
可得圆的直角坐标方程:$(x+\sqrt{2})^{2}$+y2=2,
化为:x2+y2+2$\sqrt{2}$x=0,化为极坐标方程为:${ρ}^{2}+2\sqrt{2}ρ$cosθ=0,
即ρ=-2$\sqrt{2}$cosθ.
故选:B.
点评 本题考查了极坐标方程与直角坐标方程的互化,考查了推理能力与计算能力,属于基础题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:解答题
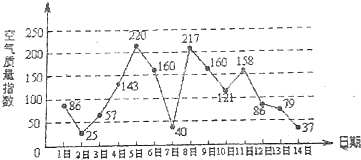 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | (x+1)2+y2=4 | D. | (x+2)2+y2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
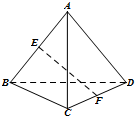 如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{1024}$ | D. | $\frac{1}{256}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+3y-4=0 | B. | 3x-2y+4=0 | C. | 2x-3y+4=0 | D. | 3x-2y+24=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com