
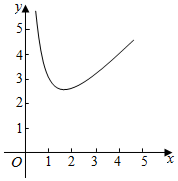
 已知函数y=x+$\frac{2}{x}$(x>0)的图象(如图所示),你能说出这个函数在哪个区间为单调函数吗?请证明你的结论.
已知函数y=x+$\frac{2}{x}$(x>0)的图象(如图所示),你能说出这个函数在哪个区间为单调函数吗?请证明你的结论. 分析 利用基本不等式求得且仅当x=$\frac{2}{x}$时,函数y取得最小值,从而求得函数的单调区间,再利用单调性与导数的关系进行证明.
解答 解:∵函数y=x+$\frac{2}{x}$(x>0),∴y≥2$\sqrt{x•\frac{2}{x}}$=2$\sqrt{2}$,当且仅当x=$\frac{2}{x}$时,取等号,
故函数y在(0,$\sqrt{2}$)上单调递减,在($\sqrt{2}$,+∞)上单调递增.
证明:在(0,$\sqrt{2}$)上,∵y′=1-$\frac{2}{{x}^{2}}$<0,故函数y=x+$\frac{2}{x}$(x>0)在(0,$\sqrt{2}$)上单调递减.
在($\sqrt{2}$,+∞)上,∵y′=1-$\frac{2}{{x}^{2}}$>0,故函数y=x+$\frac{2}{x}$(x>0)在($\sqrt{2}$,+∞)上单调递增.
点评 本题主要考查基本不等式,函数的单调性的判断和证明,单调性与导数的关系,属于中档题.


科目:高中数学 来源: 题型:解答题
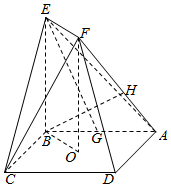 如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18+36$\sqrt{5}$ | B. | 54+18$\sqrt{5}$ | C. | 90 | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{2}$个单位长度 | B. | -π个单位长度 | C. | π个单位长度 | D. | $\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )
某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )| A. | 各月的平均最低气温都在0℃以上 | |
| B. | 七月的平均温差比一月的平均温差大 | |
| C. | 三月和十一月的平均最高气温基本相同 | |
| D. | 平均最高气温高于20℃的月份有5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\sqrt{3}$+2 | C. | -$\sqrt{3}$-2 | D. | $\sqrt{3}$-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com