
分析 由椭圆$\frac{x^2}{m}+\frac{y^2}{3}=1$的两个焦点F1,F2都在x轴上,得m>3,正弦定理得:$\frac{|P{F}_{2}|+|P{F}_{1}|}{|{F}_{1}{F}_{2}|}$=$\frac{2a}{2c}$=2,由此能求出m.
解答 解:∵椭圆$\frac{x^2}{m}+\frac{y^2}{3}=1$的两个焦点F1,F2都在x轴上,∴m>3,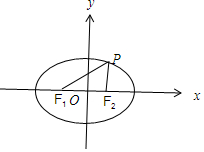
∵P是第一象限内该椭圆上的一点,且$\frac{{sin∠P{F_1}{F_2}+sin∠P{F_2}{F_1}}}{{sin∠{F_1}P{F_2}}}=2$,
∴由正弦定理得:$\frac{|P{F}_{2}|+|P{F}_{1}|}{|{F}_{1}{F}_{2}|}$=$\frac{2a}{2c}$=2,
∴e=$\frac{c}{a}=\frac{\sqrt{m-3}}{\sqrt{m}}$=$\frac{1}{2}$,
解得m=4.
故答案为:4.
点评 本题考查正数值的求法,考查椭圆、离心率、正弦定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=ln|x| | C. | y=sin($\frac{π}{2}$-x) | D. | y=-x2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 阅读程序框图,并完成下列问题:
阅读程序框图,并完成下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | 10 | 8 | 6 | 5 |
| A. | 30 | B. | 40 | C. | 45 | D. | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com